Exam 2: Applications of the Derivative
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
A health food store stocks bottles of multivitamins. It orders equal quantities of stock from its wholesaler at equally spaced points throughout the year. The cost of replacing each order is $250. Moreover, the cost of keeping a jar of vitamins in inventory is $1 per year. The store predicts that it will sell 12,500 bottles of vitamins in the next year. How many orders of how many bottles each will result in a minimum cost to the health food store?
Enter your answer exactly as: a, b (integers) where a represents the number of orders and b represents the number of bottles in each order (no units or words).
(Short Answer)
5.0/5  (40)
(40)
A toll road averages 36,000 cars per day when charging $1 (100 cents) per car. A survey concludes that changing the toll will result in 300 fewer cars for each cent of increase in price. Which of the following represents the revenue that will result from an increase of x cents in the price of the toll?
(Multiple Choice)
4.9/5  (31)
(31)
An open box with square ends is to be constructed with a volume of 125 cubic inches. The bottom is to be made of a material that weighs twice as much per square inch as the material used for the sides. What should the dimensions of the box be in order to minimize its weight? (Note: the actual weights of the materials do not matter.)Enter your answer exactly as a, b, c where these integers represent length, width, and height (no units or × symbols)
(Short Answer)
4.8/5  (31)
(31)
Suppose f(x) is the function graphed below. Which of the following is f(x)? 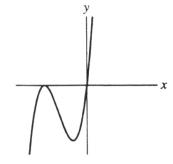
(Multiple Choice)
4.9/5  (32)
(32)
A rectangular corral with a total area of 60 square meters is to be fenced off and then divided into 2 rectangular sections by a fence down the middle. 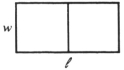 The fencing for the outside costs $9 per running meter, whereas that for the interior dividing fence costs $12 per running meter. Which of the following statements hold, if the cost (c) of the fencing is to be maximized? (I) The constraint equation is 3w + 2 l = 60 .
(II) The objective equation is 2l ∙ w = 60 .
(III) The constraint equation is w ∙ l = 60 .
(IV) The objective equation is C = 30w + 18l .
(V) The constraint equation is C = 12w + 9wl .
(VI) The objective equation is C = 60 - lw .
The fencing for the outside costs $9 per running meter, whereas that for the interior dividing fence costs $12 per running meter. Which of the following statements hold, if the cost (c) of the fencing is to be maximized? (I) The constraint equation is 3w + 2 l = 60 .
(II) The objective equation is 2l ∙ w = 60 .
(III) The constraint equation is w ∙ l = 60 .
(IV) The objective equation is C = 30w + 18l .
(V) The constraint equation is C = 12w + 9wl .
(VI) The objective equation is C = 60 - lw .
(Multiple Choice)
4.7/5  (29)
(29)
Determine all the values of x where relative maximum and minimum points of the function occur. Distinguish the maxima from the minima using the second derivative rule. Enter your answer exactly as: f(a) rel max, f(b) rel min in that order.
(Short Answer)
4.8/5  (43)
(43)
Which of the following is (are) true of
(I) f is decreasing on (1, ?)
(II) (1, f(1)) is a relative minimum point
(III) f is concave down everywhere
(IV) (0, 0) is an inflection point
(Multiple Choice)
4.7/5  (37)
(37)
Determine all maximum and minimum values of f(x) = - + 3 + 9x - 1 on Enter your answer exactly as: a,b both integers where a is the minimum of f and b is the maximum of f.
(Short Answer)
4.8/5  (55)
(55)
Showing 81 - 93 of 93
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)