Exam 6: The Definite Integral
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Determine if the function F is the general antiderivative of the function f. F(t) = 5t2 + 3et + C;  f(t) = 10t + 3e
f(t) = 10t + 3e
Free
(True/False)
4.9/5  (34)
(34)
Correct Answer:
True
Refer to the information in the graph below. Set up a definite integral or sum of definite integrals that gives the area of the shaded portion. 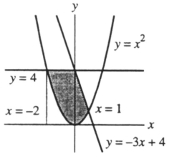
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
D
Find the area of the region bounded by y = x and y = .
Enter a reduced fraction .
Free
(Short Answer)
4.8/5  (40)
(40)
Correct Answer:
Find all antiderivatives of the function.
-f(y) = Enter your answer as a polynomial in y in standard form.
(Short Answer)
4.8/5  (40)
(40)
Given f(x) = + x +1 on the interval 0 ≤ x ≤ 4 and with n = 5, compute the Riemann sum (a) using the left endpoints; (b) using the right endpoints; and (c) using the midpoints of the subintervals. Enter your answer as just a, b, c all integers separated by commas.
Enter the numbers in the order that answers (a), (b), (c) but do not label. Round to the nearest whole number.
(Short Answer)
4.7/5  (29)
(29)
Find the volume of the solid of revolution generated by revolving the region formed by the graphs of and about the x-axis.
Enter a reduced quotient . 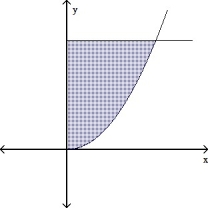
(Short Answer)
4.8/5  (38)
(38)
Find the area of the region between y = 3x - 1, the y-axis, and the lines y = 2 and .
(Multiple Choice)
4.9/5  (35)
(35)
Find: dx
Enter a polynomial in x in standard form with any fractional coefficients or powers in reduced form .
(Short Answer)
4.8/5  (34)
(34)
Given the graph of the function y = , set up the definite integral that gives the area of the shaded region. 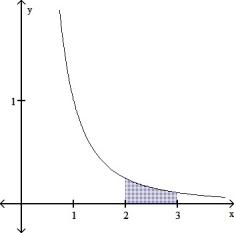
(Multiple Choice)
4.8/5  (39)
(39)
Find the area of the region bounded by the curve y = , the y-axis, and the line y = 1.
(Multiple Choice)
4.9/5  (34)
(34)
Use a Riemann sum to approximate the area under the graph of f(x) on the given interval. Use the right endpoints.
Enter just an integer.
f(x) = 2x + 1; 1 ≤ x ≤ 5, n = 4
(Short Answer)
4.8/5  (35)
(35)
This is a sketch of the region between the two curves y = and y = 2 and the x-axis. Does the following represent the area of the region? 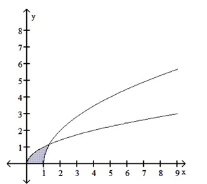
(True/False)
4.8/5  (44)
(44)
Given the graph of the function y = + 8, set up the definite integral that gives the area of the shaded region. 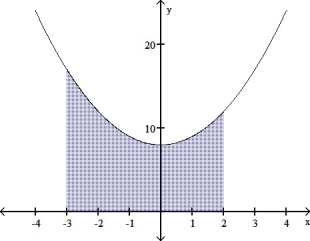
(Multiple Choice)
4.8/5  (27)
(27)
For the Riemann sum, [5 + 5 + 5 + 5 + 5 ](0.4); a = 1, determine n, b, and f(x).
Enter your answer as just n, b, f(x) (2 integers in that order separated by commas and followed by a power function in x).
(Short Answer)
4.8/5  (33)
(33)
Determine the area under the curve y = 4x + 4 from x = 2 to x = 3.
Enter an integer.
(Short Answer)
4.7/5  (27)
(27)
This is a sketch of the region between the two curves and . Does the following represent the area of the region? 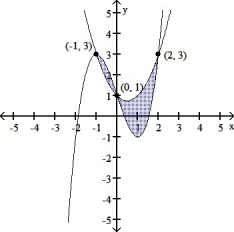
(True/False)
4.8/5  (31)
(31)
Find the value of k that makes the antidifferentiation formula true.
- = k ln|7 - x| + C
(Multiple Choice)
4.7/5  (42)
(42)
Showing 1 - 20 of 135
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)