Exam 11: Taylor Polynomials and Infinite Series
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Determine the sum of the following infinite series: Enter just a reduced fraction of form .
(Short Answer)
4.7/5  (40)
(40)
Sum an appropriate infinite series to find the rational number whose decimal expansion is: .
Enter just a reduced fraction of form .
(Short Answer)
4.8/5  (30)
(30)
Find an infinite series that converges to the value of dx. Is correct?
(True/False)
4.9/5  (32)
(32)
Use the integral test to determine whether the infinite series is convergent or divergent.
Enter just "convergent" or "divergent".
(Short Answer)
4.9/5  (30)
(30)
Determine the sum of the following geometric series: 3 - 1.8 + 1.08 + .648 - ... .
Enter just a real number rounded off to three decimal places.
(Short Answer)
4.9/5  (33)
(33)
Find the third Taylor polynomial of f(x) = + sin x at x = 0.
Enter an unlabeled polynomial in x in standard form (i.e., highest powers first).
(Short Answer)
4.8/5  (38)
(38)
Find the first four non-zero terms of the Taylor series at x = 0 of .
Is the correct answer?
(True/False)
4.7/5  (36)
(36)
Suppose f(x) = - 7 + 2. The third Taylor polynomial of f(x) at x = 0 is .
(True/False)
4.9/5  (44)
(44)
Determine the first four non-zero terms of the Taylor series at x = 0 for f(x) = sin .
Is the correct answer?
(True/False)
4.8/5  (32)
(32)
Find the third Taylor polynomial of f(x) = sin x at x = 0 and use it to approximate .
Enter just a real number rounded off to two decimal places.
(Short Answer)
4.7/5  (45)
(45)
The area of a circle with radius 1 is π. If f(x) = gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct? 2()=1- \approx 1- = so \pi\approx 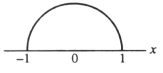
(True/False)
4.9/5  (47)
(47)
Determine the sum of the following geometric series: .
Enter a reduced fraction of form .
(Short Answer)
4.7/5  (37)
(37)
Find the Taylor series expansion for f(x) = and use it to determine which of the following is false?
(Multiple Choice)
4.8/5  (38)
(38)
Find the first four non-zero terms of the Taylor series at x = 0 of .
Is correct?
(True/False)
4.9/5  (32)
(32)
Use the integral test to determine whether the infinite series is convergent or divergent.
Enter just "convergent" or "divergent".
(Short Answer)
4.9/5  (34)
(34)
Estimate by using the second Taylor polynomial for f(x) = . Is the solution?
(True/False)
4.8/5  (36)
(36)
Determine the sum of the geometric series - + - ..., if it is convergent.
(Multiple Choice)
4.8/5  (31)
(31)
Find the third Taylor polynomial of f(x) = cos x at x = .
Enter your answer as an unlabeled polynomial in x - in standard form (i.e., highest powers first).
(Short Answer)
4.8/5  (42)
(42)
Showing 41 - 60 of 132
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)