Exam 3: Matrices
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Use inverse matrices to solve the system of linear equations.
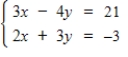
Free
(Multiple Choice)
4.9/5  (46)
(46)
Correct Answer:
B
Suppose that the economy of a small nation has an electronics industry, a steel industry, and an auto industry, with the following technology matrix.

If the nation wishes to have surpluses of 104 units of electronics production, 271 units of steel production, and 200 automobiles, find the gross production of each industry.
If the nation wishes to have surpluses of 104 units of electronics production, 271 units of steel production, and 200 automobiles, find the gross production of each industry.
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
E
The following technology matrix describes the relationship of certain industries within the economy to each other. (A&F, agriculture and food; RM, raw materials; M, manufacturing; F, fuels industry; U, utilities; SI, service industries) 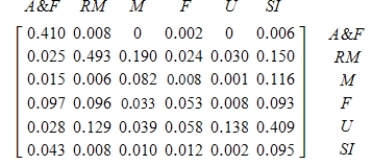
How many units of fuels were required to produce 1,000 units of manufactured goods?
How many units of fuels were required to produce 1,000 units of manufactured goods?
(Multiple Choice)
4.8/5  (41)
(41)
Consider the original budget matrix. Assume there is a 20% increase in manufacturing, a 4% increase in office, a 6% increase in sales, a 21% increase in shipping, a 5% increase in accounting, and a 4% decrease in management. Find the new budget matrix by developing a matrix A to represent these departmental increases and then computing the matrix BA. 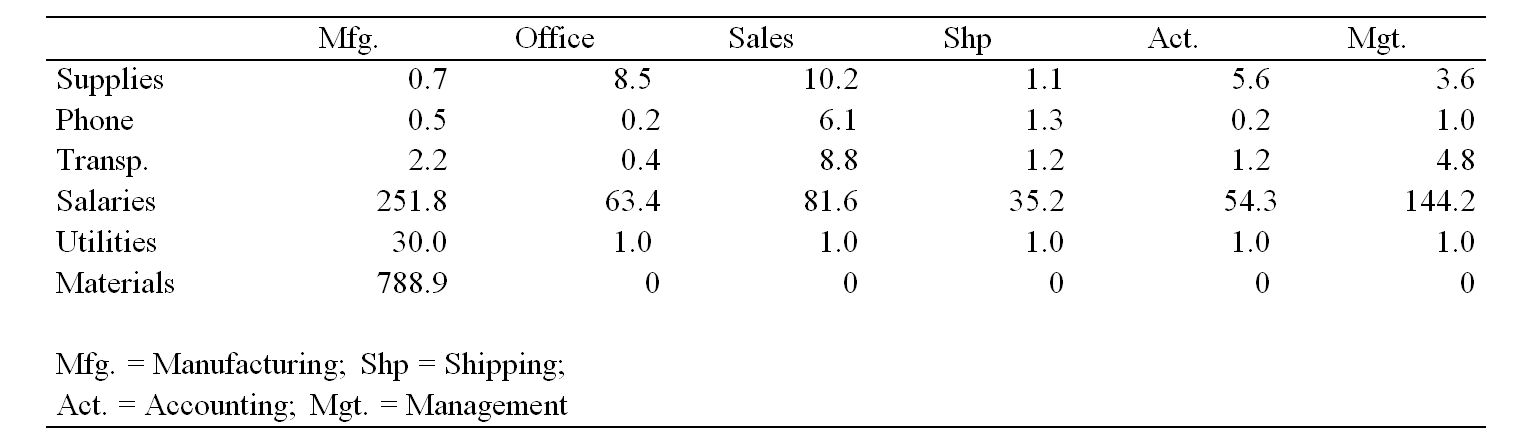
(Multiple Choice)
4.8/5  (31)
(31)
Solve the following system of equations for y. This gives a formula for solving two equations in two variables for y.
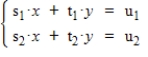
(Multiple Choice)
4.9/5  (28)
(28)
The matrix that follows represents work efficiency for workers at nine different work centers. Suppose that the work centers changes in rules cause efficiency to decrease by 0.04 at work centers 2 and 5 and to decrease by 0.01 at work center 7. Write the matrix that describes the new efficiencies.
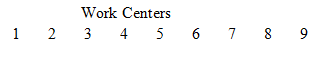

(Multiple Choice)
4.8/5  (32)
(32)
A system of equations may have a unique solution, an infinite number of solutions, or no solution. Use matrices to find the general solution of the following system, if a solution exists. 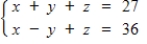
(Multiple Choice)
4.8/5  (36)
(36)
A clothing manufacturer has factories in Atlanta, Chicago, and New York. Sales (in thousands) during the first quarter are summarized in the matrix below. 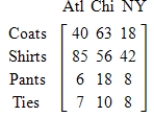
During this period, the selling price of a coat was $125, of a shirt $50, of a pair of pants $50, and of a tie $25. Use matrix multiplication to find the total revenue received by each factory.
During this period, the selling price of a coat was $125, of a shirt $50, of a pair of pants $50, and of a tie $25. Use matrix multiplication to find the total revenue received by each factory.
(Multiple Choice)
4.9/5  (30)
(30)
The following tables give the rank and number of registered dogs for the top ten breeds for 1995 and their 2002 data. Which breed had the greatest improvement in rank? 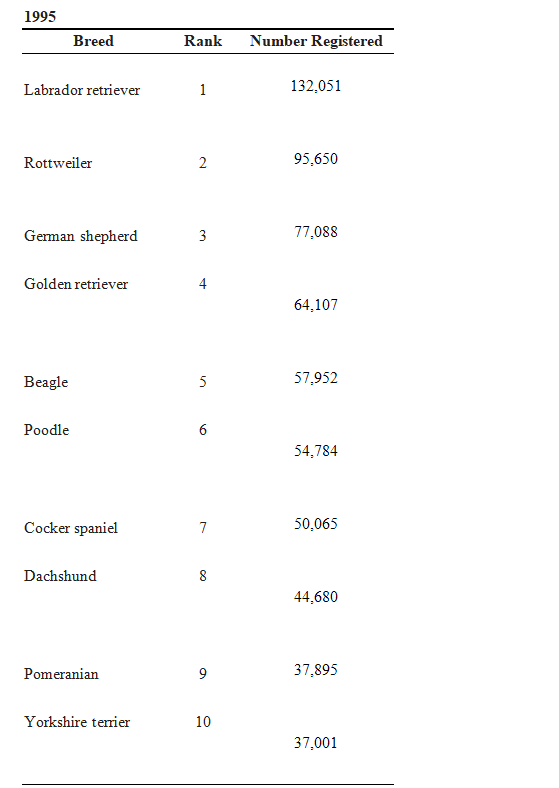
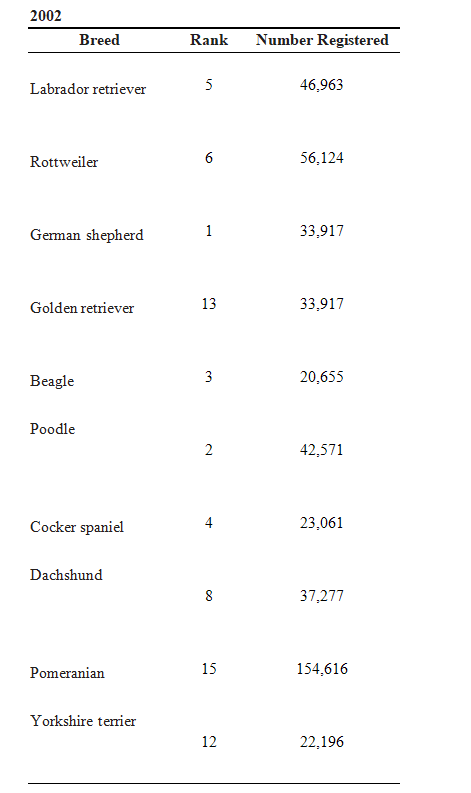
(Multiple Choice)
4.8/5  (38)
(38)
We have encoded messages by assigning the letters of the alphabet the numbers 1-26, with a blank assigned the number 27, and by using an encoding matrix A that converts the numbers to the coded message. To decode any message encoded by A, we must find the inverse of A, denoted by A-1, and multiply A-1 times the coded message. Use this code and the given encoding matrix A to find the matrix that can be used to decode the given message.
The code matrix is 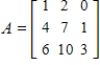 . The message is 33, 132, 214, 22, 110, 203, 34, 132, 201.
. The message is 33, 132, 214, 22, 110, 203, 34, 132, 201.
(Multiple Choice)
4.9/5  (40)
(40)
The tables below give the numbers of some species of threatened and endangered wildlife in the United States and in foreign countries in 2003. Let A represent the matrix that contains the number of each of these species in the United States in 2003 and B represent the matrix that contains the number of each of these species outside the United States in 2003. Find the matrix B - A. What do the negative entries in matrix B - A mean?
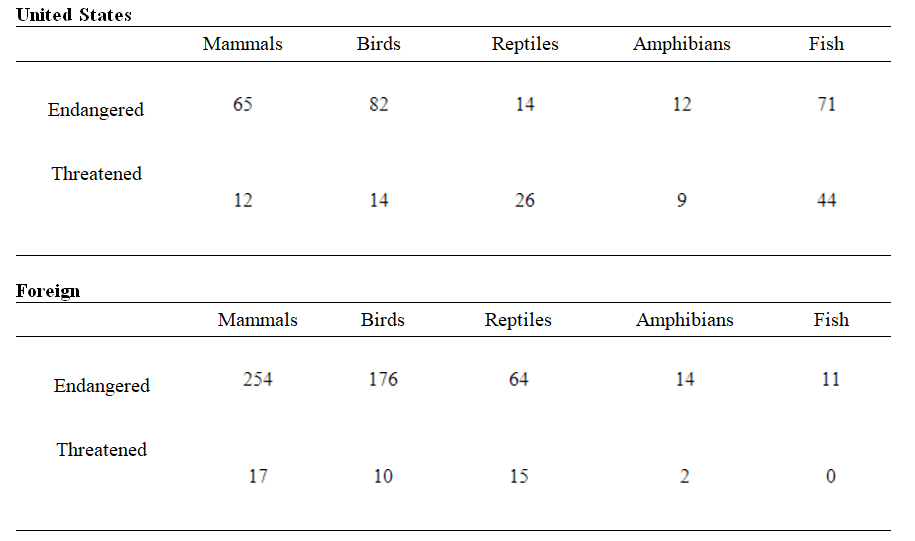
(Multiple Choice)
4.9/5  (41)
(41)
The given matrix is an augmented matrix representing a system of linear equations. Find the solution of the system. 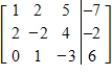
(Multiple Choice)
4.9/5  (42)
(42)
A closed model for an economy identifies government, the profit sector, the nonprofit sector, and households as its industries. Each unit of government output requires 0.3 unit of government input, 0.2 unit of profit sector input, 0.2 unit of nonprofit sector input, and 0.4 unit of households input. Each unit of profit sector output requires 0.2 unit of government input, 0.3 unit of profit sector input, 0.2 unit of nonprofit sector input, and 0.4 unit of households input. Each unit of nonprofit sector output requires 0.2 unit of government input, 0.2 unit of profit sector input, 0.2 unit of nonprofit sector input, and 0.6 unit of households input. Each unit of households output requires 0.05 unit of government input, 0.2 unit of profit sector input, 0.2 unit of nonprofit sector input, and 0.25 unit of households input. Write the augmented matrix for this closed model of the economy.
(Multiple Choice)
4.7/5  (29)
(29)
Use row operations on the augmented matrix to solve the given system of linear equations. 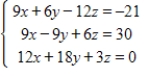
(Multiple Choice)
4.7/5  (38)
(38)
The following technology matrix describes the relationship of certain industries within the economy to each other. (A&F, agriculture and food; RM, raw materials; M, manufacturing; F, fuels industry; U, utilities; SI, service industries) 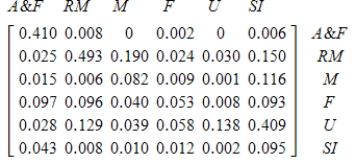
Which is most dependent on the service industry?
Which is most dependent on the service industry?
(Multiple Choice)
4.8/5  (33)
(33)
We have encoded messages by assigning the letters of the alphabet the numbers 1-26, with a blank assigned the number 27, and by using an encoding matrix A that converts the numbers to the coded message. To decode any message encoded by A, we must find the inverse of A, denoted by A-1, and multiply A-1 times the coded message. Use this code and the given encoding matrix A to find the matrix that can be used to decode the given message.
Code matrix is
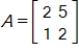 The message is
138, 59, 72, 29, 143, 58, 57, 24, 101, 44
The message is
138, 59, 72, 29, 143, 58, 57, 24, 101, 44
(Multiple Choice)
4.9/5  (23)
(23)
Showing 1 - 20 of 230
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)