Exam 4: Inequalities and Linear Programming
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Two foods contain only proteins, carbohydrates, and fats. Food A costs $1.30 per pound and contains 30% protein and 50% carbohydrates. Food B costs $1.95 per pound and contains 20% protein and 75% carbohydrates. What combination of these two foods provides at least 1 pound of protein, 2.5 pounds of carbohydrates, and 0.25 pounds of fat at the lowest cost? Round your answer to the nearest cent.
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
A
Apex Motors manufactures luxury cars and sport utility vehicles. The most likely customers are high-income men and women, and company managers want to initiate an advertising campaign targeting these groups. They plan to run 1-minute spots on business/investment programs, where they can reach 7 million women and 4 million men from their target groups. They also plan 1-minute spots during sporting events, where they can reach 2 million women and 12 million men from their target groups. Apex feels that the ads must reach at least 40 million women and at least 24 million men who are prospective customers. Let x represent the number of minutes of business/investment program commercials and y represent the number of minutes of sporting events commercials. Write the inequalities that describe the constraints on the number of each type of 1-minute spots needed to reach these target groups.
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
E
A candidate wishes to use a combination of radio and television advertisements in her campaign. Assume that each 1-minute spot on television reaches to 0.0945 million people and that each 1-minute spot on radio reaches to 0.003 million. The candidate feels she must reach at least 8.775 million people, and she must buy total of at least 85 minutes of advertisements. How many minutes of each medium should be used to minimize costs if television costs $450 per minute and radio costs $75 per minute? Round your answer to nearest integer if necessary.
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
B
A car rental agency has a budget of $1.8 million to purchase at most 100 new cars. The agency will purchase either compact cars at $15,000 each or luxury cars at $30,000 each. From past rental patterns, the agency decides to purchase at most 50 luxury cars and expects an annual profit of $8,000 per compact car and $13,500 per luxury car. How many of each type of car should be purchased in order to obtain the maximum profit while satisfying budgetary and other planning constraints? Find the maximum profit. Round your profit to the nearest dollar and another answers - to the nearest whole number.
(Multiple Choice)
4.9/5  (40)
(40)
Use the simplex method to maximize the given function. Assume all variables are nonnegative.
Maximize 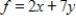 subject to
subject to
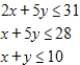
(Multiple Choice)
4.9/5  (32)
(32)
An experiment that involves learning in animals requires placing white mice and rabbits into separate, controlled environments, environment I and environment II. The maximum amount of time available in environment I 400 is minutes, and the maximum amount of time available in environment II is 500 minutes. The white mice must spend 11 minutes in environment I and 40 minutes in environment II, and the rabbits must spend 35 minutes in environment I and 50 minutes in environment II. Write a system of inequalities that describes the constraints on the number of each type of animal used in the experiment. Let x denote the number of white mice and y denote the number of rabbits.
(Multiple Choice)
4.8/5  (27)
(27)
Use technology to solve the problem.
Minimize 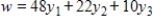 subject to
subject to
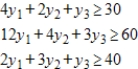
(Multiple Choice)
4.8/5  (32)
(32)
Write the dual maximization problem.
Minimize 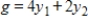 subject to
subject to
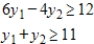
(Multiple Choice)
4.8/5  (34)
(34)
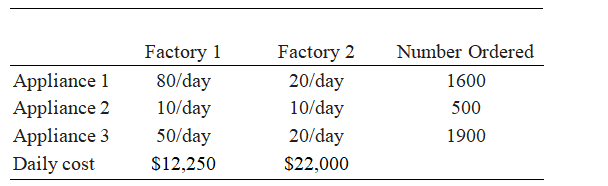
Two factories produce three different types of kitchen appliances. The following table summarizes the production capacities, the numbers of each type of appliance ordered, and the daily operating costs for the factories. How many days should each factory operate to fill the orders at minimum cost? Find the minimum cost.
(Multiple Choice)
4.9/5  (36)
(36)
Johnson City Cooperage manufactures 30-gallon and 55-gallon fiber drums. Each 30-gallon drum takes 30 minutes to make, each 55-gallon drum takes 40 minutes to make, and the company has at most 10,000 minutes available each week. Also, workplace limitations and product demand indicate that the number of 55-gallon drums produced plus half the number of 30-gallon drums produced should be at least 160, and the number of 30-gallon drums should be at least twice the number of 55-gallon drums. If Johnson City Cooperage's manufacturing costs are $4.4 for each 30-gallon drum and $6.9 for each 55-gallon drum, how many of each drum should be made each week to satisfy the constraints at minimum cost? Find the minimum cost.
(Multiple Choice)
4.9/5  (31)
(31)
Use the simplex method to find the optimal solution.
Maximize 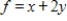 subject to
subject to 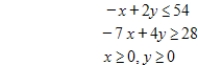
(Multiple Choice)
4.7/5  (32)
(32)
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,501 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $40 for soybeans. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.8/5  (42)
(42)
At one of its factories, a jeans manufacturer makes two styles: #891 and #917. Each pair of style-891 takes 10 minutes to cut out and 20 minutes to assemble and finish. Each pair of style-917 takes 10 minutes to cut out and 30 minutes to assemble and finish. The plant has enough workers to provide at most 7,500 minutes per day for cutting and at most 19,500 minutes per day for assembly and finishing. The profit on each pair of style-891 is $6.00 and the profit on each pair of style-917 is $9.50. Find the maximum daily profit. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.7/5  (34)
(34)
A farm co-op has 6,001 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1 hour of labor to harvest. The co-op has available at most 40,500 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $45 for soybeans. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.8/5  (27)
(27)
Use the simplex method, Excel, or another technology to solve.
Maximize 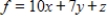 subject to
subject to 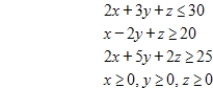
(Multiple Choice)
4.8/5  (36)
(36)
In a laboratory experiment, two separate foods are given to experimental animals. Each food contains essential ingredients, A and B, for which the animals have a minimum requirement, and each food also has an ingredient C, which can be harmful to the animals. The table below summarizes this information.

Determine how many grams of foods 1 and 2 should be given in order to satisfy the requirements for A and B while minimizing the amount of ingredient C ingested. Also determine the minimum amount of ingredient C ingested. Round your answer to one decimal place if necessary.
Determine how many grams of foods 1 and 2 should be given in order to satisfy the requirements for A and B while minimizing the amount of ingredient C ingested. Also determine the minimum amount of ingredient C ingested. Round your answer to one decimal place if necessary.
(Multiple Choice)
4.9/5  (36)
(36)
Suppose a ball manufacturer produces soccer balls, footballs, and volleyballs. The manager feels that restricting the types of balls produced could increase revenue. The following table gives the price of each ball, the raw materials cost, and the profit on each ball. The monthly profit must be at least $40,000, and the raw materials costs must be no more than $50,000. How many of each type of ball should be produced to maximize the revenue? What is the maximum revenue?
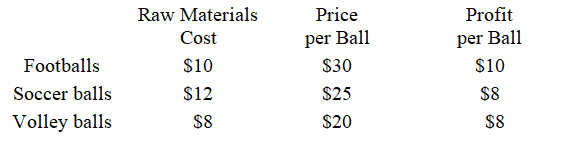
(Multiple Choice)
4.9/5  (37)
(37)
Solve both the primal and dual problems with the simplex method. Use f to represent the dual objective function.
Minimize 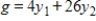 subject to
subject to
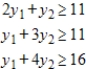
(Multiple Choice)
4.9/5  (31)
(31)
Suppose that in a hospital ward, the patients can be grouped into two general categories depending on their condition and the amount of solid foods they require in their diet. A combination of two diets is used for solid foods because they supply essential nutrients for recovery. The table below summarizes the patient groups and their minimum daily requirements. Let x represent the number of servings of A and y represent the number of servings of B. Determine the inequalities that describe how many servings of each diet are needed to provide the nutritional requirements and then graph the region determined by these constraint inequalities.
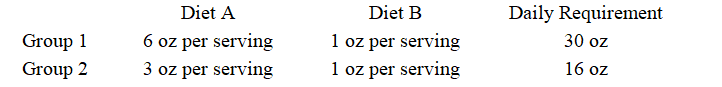
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)