Exam 13: A: Definite Integrals - Techniques
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
A 58-year-old couple are considering opening a business of their own. They will either purchase an established Gift and Card Shoppe or open a new Video Rental Palace. The Gift Shoppe has a continuous income stream with an annual rate of flow at time t given by 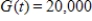 (dollars per year) and the Video Palace has a continuous income stream with a projected annual rate of flow at time t given by
(dollars per year) and the Video Palace has a continuous income stream with a projected annual rate of flow at time t given by 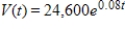 (dollars per year). The initial investment is the same for both businesses, and money is worth 10% compounded continuously. Determine which is the better buy by finding the present value of each business over the next 6 years (until the couple reach age 64).
(dollars per year). The initial investment is the same for both businesses, and money is worth 10% compounded continuously. Determine which is the better buy by finding the present value of each business over the next 6 years (until the couple reach age 64).
(Multiple Choice)
4.9/5  (38)
(38)
The production from a particular assembly line is considered a continuous income stream with annual rate of flow given by 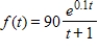 (in thousands of dollars per year). Use Simpson's Rule with n = 4 to approximate the total income to 2 decimal places over the first 2 years, given by
(in thousands of dollars per year). Use Simpson's Rule with n = 4 to approximate the total income to 2 decimal places over the first 2 years, given by 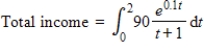 .
.
(Multiple Choice)
4.8/5  (37)
(37)
-The probability density function for the life span of an electronics part is 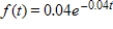 where t is the number of months in service. Find the probability that any given part of this type lasts longer than 18 months. Round your answer to three decimal places.
where t is the number of months in service. Find the probability that any given part of this type lasts longer than 18 months. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
The Carter Car Service franchise has a continuous income stream with a monthly rate of flow modeled by 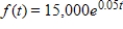 (dollars per month). Find the average flow of income over years 4 to 5. Round your answer to the nearest cent.
(dollars per month). Find the average flow of income over years 4 to 5. Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (34)
(34)
The demand function for a product is 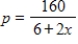 , where p is the number of dollars and x is the number of units. If the equilibrium quantity is $7, what is the consumer's surplus? Round your answer to two decimal places.
, where p is the number of dollars and x is the number of units. If the equilibrium quantity is $7, what is the consumer's surplus? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (36)
(36)
Suppose that the income from a slot machine in a casino flows continuously at a rate of 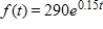 , where t is the time in hours since the casino opened. The total income during the first 8 hours is given by
, where t is the time in hours since the casino opened. The total income during the first 8 hours is given by 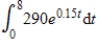 . Find the average income over the first 8 hours.
. Find the average income over the first 8 hours.
(Multiple Choice)
4.9/5  (43)
(43)
Use the Trapezoidal Rule to approximate 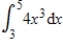 with n = 6. Round your answer to two decimal places.
with n = 6. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Suppose that the rate at which a nuclear power plant produces radioactive waste is proportional to the number of years it has been operating, according to 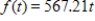 in pounds per year. Suppose also that the waste decays exponentially at a rate of 9% per year. Then the amount of radioactive waste that will accumulate in b years is given by
in pounds per year. Suppose also that the waste decays exponentially at a rate of 9% per year. Then the amount of radioactive waste that will accumulate in b years is given by 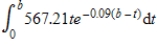 . Evaluate this integral.
. Evaluate this integral.
(Multiple Choice)
4.8/5  (38)
(38)
True or false. For the function 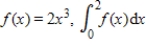 gives the area between the graph of
gives the area between the graph of 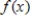 and the x-axis from
and the x-axis from  .
.
(True/False)
4.9/5  (32)
(32)
Find the area of the shaded region for the graph given below. 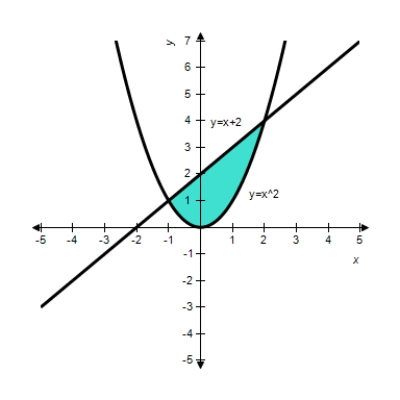
(Multiple Choice)
4.9/5  (38)
(38)
Assume that a store finds that its sales revenue changes at a rate given by 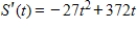 dollars per day, where t is the number of days after an advertising campaign ends and
dollars per day, where t is the number of days after an advertising campaign ends and 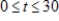 . Find the total sales for the second week after the campaign ends
. Find the total sales for the second week after the campaign ends 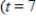 to
to 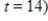 .
.
(Multiple Choice)
4.9/5  (32)
(32)
The average life for a particular brand of car battery is given by the following probability density function where t is in years. 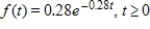 Find the probability that a battery chosen at random lasts between 2 and 7 years. Round your answer to two decimal places.
Find the probability that a battery chosen at random lasts between 2 and 7 years. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Assume that a store finds that its sales revenue changes at a rate given by 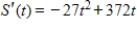 dollars per day, where t is the number of days after an advertising campaign ends and
dollars per day, where t is the number of days after an advertising campaign ends and 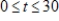 . Find the total sales for the second week after the campaign ends
. Find the total sales for the second week after the campaign ends 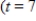 to
to 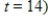 .
.
(Multiple Choice)
4.7/5  (33)
(33)
Use integration by parts to evaluate 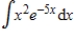 . Note that evaluation may require integration by parts more than once.
. Note that evaluation may require integration by parts more than once.
(Multiple Choice)
4.9/5  (44)
(44)
A transmission repair firm that wants to offer a lifetime warranty on its repairs has determined that the probability density function for transmission failure after repair is 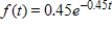 , where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
, where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
(Multiple Choice)
4.7/5  (40)
(40)
A drug manufacturer has developed a time-release capsule with the number of milligrams of the drug in the bloodstream given by 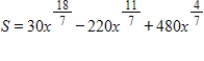 where x is in hours and
where x is in hours and 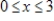 . Find the average number of milligrams of the drug in the bloodstream for the first 3 hours after a capsule is taken. Round your answer to the nearest milligram.
. Find the average number of milligrams of the drug in the bloodstream for the first 3 hours after a capsule is taken. Round your answer to the nearest milligram.
(Multiple Choice)
4.8/5  (31)
(31)
Consider the following supply and demand schedules, with p in dollars and x as the number of units. 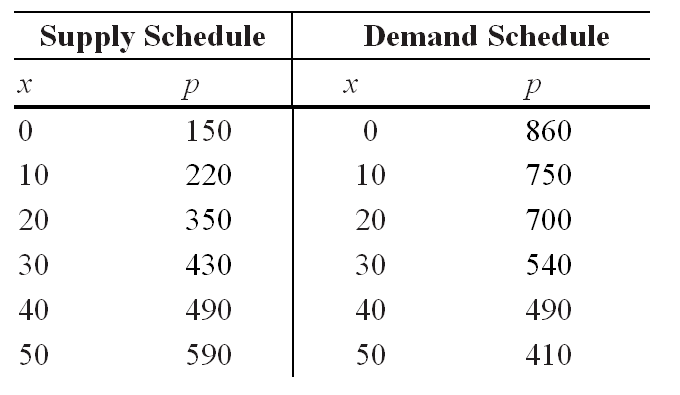 Use Simpson's Rule to approximate the producer's surplus at market equilibrium to 2 decimal places. Note that market equilibrium can be found from the tables.
Use Simpson's Rule to approximate the producer's surplus at market equilibrium to 2 decimal places. Note that market equilibrium can be found from the tables.
(Multiple Choice)
4.8/5  (35)
(35)
Suppose that the demand for q units of a certain product at p per unit is given by 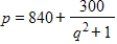 . Use Simpson's Rule with n = 6 to approximate the average price as demand ranges from 3 to 8 items to the nearest cent.
. Use Simpson's Rule with n = 6 to approximate the average price as demand ranges from 3 to 8 items to the nearest cent.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 41 - 60 of 370
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)