Exam 6: Trigonometric Functions: Right Triangle Approach
Exam 1: Fundamentals229 Questions
Exam 2: Functions98 Questions
Exam 3: Polynomial and Rational Functions145 Questions
Exam 4: Exponential and Logarithmic Functions99 Questions
Exam 5: Trigonometric Functions: Unit Circle Approach100 Questions
Exam 6: Trigonometric Functions: Right Triangle Approach119 Questions
Exam 7: Analytic Trigonometry119 Questions
Exam 8: Polar Coordinates and Parametric Equations109 Questions
Exam 9: Vectors in Two and Three Dimensions96 Questions
Exam 10: Systems of Equations and Inequalities140 Questions
Exam 11: Conic Sections99 Questions
Exam 12: Sequences and Series100 Questions
Exam 13: Limits: a Preview of Calculus66 Questions
Select questions type
A satellite passes over two tracking stations, and , km apart. When the satellite is between the two stations the angles of elevation at the stations are measured as and respectively. What is the distance , between the satellite and station .
(Essay)
4.9/5  (21)
(21)
How many revolutions will a bicycle wheel of diameter 26 inches make as the bicycle travels a distance of miles?
(Essay)
4.7/5  (39)
(39)
Use a calculator to find an approximate value of each expression correct to five decimal places, if it is defined.
(a)
(b)
(Essay)
4.8/5  (31)
(31)
Use a calculator to find an approximate value of each expression correct to five decimal places, if it is defined.
(a)
(b)
(Essay)
4.9/5  (37)
(37)
At a point ft from the base of a building, the angles of elevation to the bottom of a radio transmission tower and to the top of the tower are and . Find the height of the radio tower to the nearest foot. 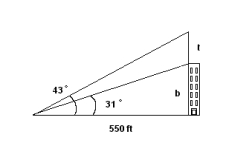
(Essay)
5.0/5  (33)
(33)
A pilot sets out from an airport and heads in the direction N W, flying at a constant speed of mi/h. Forty-five minutes later the pilot makes a course and speed correction and now heads in the direction N W and reduces her speed to mi/h. Half an hour later, engine trouble forces her to make an emergency landing. Find the distance between the airport and the final landing point.
(Essay)
4.9/5  (41)
(41)
A 22-ft ladder leans against a building so that the angle between the ground and the ladder is . How high does the ladder reach on the building?
(Short Answer)
4.8/5  (28)
(28)
Use a calculator to find an approximate value of each expression correct to five decimal places, if it is defined.
(a)
(b)
(Essay)
4.7/5  (31)
(31)
Find an angle between and that is coterminal with each angle given.
a. b. c.
(Essay)
4.7/5  (32)
(32)
Showing 41 - 60 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)