Exam 13: Limits: a Preview of Calculus
Exam 1: Fundamentals229 Questions
Exam 2: Functions98 Questions
Exam 3: Polynomial and Rational Functions145 Questions
Exam 4: Exponential and Logarithmic Functions99 Questions
Exam 5: Trigonometric Functions: Unit Circle Approach100 Questions
Exam 6: Trigonometric Functions: Right Triangle Approach119 Questions
Exam 7: Analytic Trigonometry119 Questions
Exam 8: Polar Coordinates and Parametric Equations109 Questions
Exam 9: Vectors in Two and Three Dimensions96 Questions
Exam 10: Systems of Equations and Inequalities140 Questions
Exam 11: Conic Sections99 Questions
Exam 12: Sequences and Series100 Questions
Exam 13: Limits: a Preview of Calculus66 Questions
Select questions type
Determine whether the sequence converges or diverges. If it converges, find the limit.
Free
(Essay)
4.8/5  (33)
(33)
Correct Answer:
Converges;
Use the definition of area as a limit to find the area of the region that lies under the graph of over the interval .
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
Width: , REP: , Height: .
For the function g whose graph is given, state the value of the given quantity if it exists. 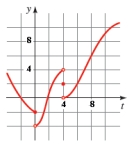 a)
b)
c)
a)
b)
c)
(Essay)
4.9/5  (35)
(35)
Use the definition of area as a limit to find the area of the region that lies under the graph of over the interval .
(Essay)
4.9/5  (28)
(28)
Use a graphing device to determine whether exists. If the limit exists, estimate its value to two decimal places.
(Essay)
4.7/5  (33)
(33)
Use a table of values to estimate the value of . Then use a graphing device to confirm your result graphically.
(Essay)
4.9/5  (25)
(25)
Determine whether the sequence converges or diverges. If it converges, find the limit.
(Essay)
4.8/5  (29)
(29)
Complete the table of values (to five decimal places) and use the table to estimate the value of . x 8.9 8.99 8.999 9.001 9.01 9.1 f(x)
(Essay)
4.9/5  (33)
(33)
Estimate the area under the graph of from to using
(a) four approximating rectangles and right endpoints.
(b) four approximating rectangles and left endpoints.
(c) eight approximating rectangles and right endpoints.
(Essay)
4.8/5  (29)
(29)
Showing 1 - 20 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)