Exam 8: Polar Coordinates and Parametric Equations

Test the polar equation for symmetry with respect to the polar axis, the pole, and the line $\theta = \pi / 2$ . $r = 5 \sec \theta$

Find the rectangular coordinates for the point whose polar coordinates are given. $( 0,11 \pi )$

Sketch a graph of the polar equation. $r = - 2 \sin 3 \theta$

For the point with polar coordinates $P ( 1 , \pi / 3 )$ find two other polar coordinate representations of P with $r > 0$

Convert the polar equation to rectangular coordinates. $r + \cos \theta = 3$

Write $- 2 ( 1 + i )$ in polar form, with $\theta$ between $0$ and $2 \pi$ .

Sketch the curve represented by $x = \frac { 1 } { 2 } t$ , $y = t ^ { 2 } + 3$ and find a rectangular-coordinate equation for the curve.

Sketch the graph of the polar equation. $r = 2 - 2 \sin \theta$

Convert the polar equation to rectangular coordinates. $r = 8 \sin \theta$

Write the product $z _ { 1 } z _ { 2 }$ , and quotient $z _ { 1 } / z _ { 2 }$ , of $z _ { 1 } = 2 \left( \cos \frac { 5 \pi } { 6 } + i \sin \frac { 5 \pi } { 6 } \right)$ and $z _ { 2 } = 5 \left( \cos \frac { \pi } { 3 } + i \sin \frac { \pi } { 3 } \right)$ in polar form.

Test the polar equation for symmetry with respect to the polar axis, the pole, and the line $\theta = \pi / 2$ . $r ^ { 2 } = \cos 2 \theta$

Find the polar coordinates of the point with rectangular coordinates $( \sqrt { 3 } , - 3 )$ .

Find parametric equations for the line of slope $2$ passing through the point $( - 2,4 )$ .

Sketch the curve represented by $x = 9 t ^ { 2 }$ , $y = 64 t ^ { 3 }$ and find a rectangular-coordinate equation for the curve.

Find the rectangular coordinates of the point with polar coordinates $( 2 , \pi / 3 )$ .

Sketch the curve represented by 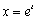, 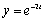and find a rectangular-coordinate equation for the curve.

Convert the equation to polar form. $y = 9 / 4$

Write $\sqrt { 2 } i$ in polar form, with $\theta$ between $0$ and $2 \pi$ .

Convert the rectangular coordinates to polar coordinates with $r > 0 \text { and } 0 \leq \theta < 2 \pi$ $( 0 , - \sqrt { 2 } )$

Write $z _ { 1 } = 1 - i$ and $z _ { 2 } = 1 - \sqrt { 3 } i$ in polar form and then find $z _ { 1 } z _ { 2 }$ , $z _ { 1 } / z _ { 2 }$ , and $1 / z _ { 1 }$ .