Exam 11: Conic Sections
Exam 1: Fundamentals229 Questions
Exam 2: Functions98 Questions
Exam 3: Polynomial and Rational Functions145 Questions
Exam 4: Exponential and Logarithmic Functions99 Questions
Exam 5: Trigonometric Functions: Unit Circle Approach100 Questions
Exam 6: Trigonometric Functions: Right Triangle Approach119 Questions
Exam 7: Analytic Trigonometry119 Questions
Exam 8: Polar Coordinates and Parametric Equations109 Questions
Exam 9: Vectors in Two and Three Dimensions96 Questions
Exam 10: Systems of Equations and Inequalities140 Questions
Exam 11: Conic Sections99 Questions
Exam 12: Sequences and Series100 Questions
Exam 13: Limits: a Preview of Calculus66 Questions
Select questions type
Find the eccentricity and identify the conic given by , sketch it and label its vertices.
(Essay)
4.9/5  (32)
(32)
Find an equation for a parabola with vertex at the origin, and with directrix .
(Essay)
4.8/5  (36)
(36)
A conic has equation .
(a) Use the discriminant to identify the conic.
(a) by graphing the conic with a graphing calculator.
(b) Confirm your answer in part
(c) Find the angle necessary to eliminate the - term.
(Essay)
4.8/5  (33)
(33)
Write a polar equation of an ellipse with eccentricity and directrix .
(Essay)
4.8/5  (43)
(43)
Complete the square to determine whether the equation represents an ellipse, a parabola, a hyperbola, or a degenerate conic. Then sketch the graph of the equation. If the graph is an ellipse, find the center, foci, vertices, and lengths of the major and minor axes. If it is a parabola, find the vertex, focus and directrix. If it is a hyperbola, find the center, foci, vertices, and asymptotes. If the equation has no graph, explain why.
(Essay)
4.7/5  (46)
(46)
Find the focus, directrix, and focal diameter of the parabola , and sketch its graph.
(Essay)
4.8/5  (41)
(41)
Find the vertices, foci, and asymptotes of the hyperbola , and sketch its graph.
(Essay)
4.8/5  (38)
(38)
Determine the - coordinates of if the axes are rotated through an angle .
(Essay)
4.9/5  (36)
(36)
Find an equation for the ellipse with endpoints of the minor axis at , and a distance of between the foci.
(Essay)
4.9/5  (42)
(42)
Write a polar equation of an ellipse with eccentricity 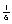 and vertex at .
and vertex at .
(Essay)
4.9/5  (36)
(36)
Use the discriminant to determine if the graph of the equation, is a parabola, an ellipse or a hyperbola, then use a rotation of axes to eliminate the - term, and sketch the graph.
(Essay)
4.9/5  (43)
(43)
Find the vertices, foci, and asymptotes of the hyperbola , and sketch its graph.
(Essay)
4.9/5  (39)
(39)
Find the focus, directrix, and focal diameter of the parabola , and sketch its graph.
(Essay)
4.9/5  (39)
(39)
Complete the square to determine whether the equation , represents an ellipse, a parabola, a hyperbola, or a degenerate conic. Then sketch the graph of the equation. If the graph is an ellipse, find the center, foci, vertices, and lengths of the major and minor axes. If it is a parabola, find the vertex, focus and directrix. If it is a hyperbola, find the center, foci, vertices, and asymptotes. If the equation has no graph, explain why.
(Essay)
4.9/5  (40)
(40)
A cannon fires a cannonball as shown in the figure. The path of the cannonball is a parabola with vertex at the highest point of the path. If the cannonball lands 800 ft from the cannon and the highest point it reaches is 1600 ft above the ground, find an equation for the path of the cannonball. Place the origin at the location of the cannon. 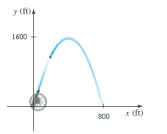
(Essay)
4.9/5  (39)
(39)
Find the vertices, foci, and eccentricity of the ellipse given by . Determine the lengths of the major and minor axes, and sketch the graph.
(Essay)
5.0/5  (39)
(39)
Showing 41 - 60 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)