Exam 7: Additional Topics in Integration
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
Suppose the time intervals between arrivals of successive cars at an expressway tollbooth during rush hour are exponentially distributed and that the average time interval between arrivals is 8 seconds. Find the probability that the average time interval between arrivals of successive cars is more than 17 seconds. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (33)
(33)
Find the function f given that the slope of the tangent line to the graph of f at any point 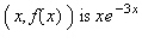 and that the graph passes through the point (0, 7).
and that the graph passes through the point (0, 7).
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the given function is a probability density function on the specified interval. 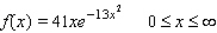
(Essay)
4.8/5  (36)
(36)
Determine whether the given function is a probability density function on the specified interval. 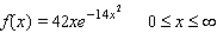
(Multiple Choice)
4.9/5  (33)
(33)
Determine the value of the constant k so that the function 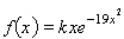 is a probability density function on the interval
is a probability density function on the interval 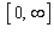 .
.
(Multiple Choice)
4.7/5  (35)
(35)
Determine whether the given function is a probability density function on the specified interval. 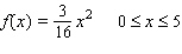
(Multiple Choice)
4.8/5  (32)
(32)
Find the expected value of the continuous random variable X associated with the probability density function over the indicated interval. 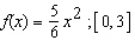
(Multiple Choice)
4.8/5  (26)
(26)
Determine the value of the constant k so that the function 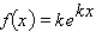 is a probability density function on the interval
is a probability density function on the interval 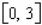 .
.
(Multiple Choice)
4.8/5  (32)
(32)
Approximate the value of the definite integral. 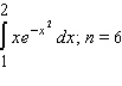 Use the trapezoidal rule. Please give the answer to four decimal places.
Use the Simpson's rule. Please give the answer to four decimal places.
Find the exact value of the integral. Please give the answer to four decimal places.
Use the trapezoidal rule. Please give the answer to four decimal places.
Use the Simpson's rule. Please give the answer to four decimal places.
Find the exact value of the integral. Please give the answer to four decimal places.
(Essay)
4.7/5  (38)
(38)
Use the table of integrals to find the integral. 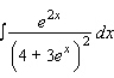 Use C as the constant of integration.
Use C as the constant of integration.
(Essay)
4.9/5  (27)
(27)
Evaluate the following improper integral whenever it is convergent. 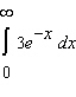
(Multiple Choice)
4.8/5  (24)
(24)
Use the table of integrals to find the integral. 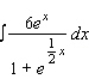 Use C as the constant of integration.
Use C as the constant of integration.
(Essay)
4.9/5  (43)
(43)
The number of voters in a certain district of a city is expected to grow at the rate of 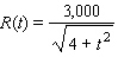 people per year
people per year 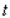 years from now. If the number of voters at present is
years from now. If the number of voters at present is 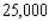 , how many voters will be in the district
, how many voters will be in the district 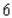 years from now?
years from now?
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the following improper integral whenever it is convergent. 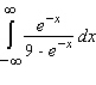 Enter divergent if the integral is divergent.
Enter divergent if the integral is divergent.
(Essay)
4.8/5  (37)
(37)
Evaluate the definite integral by using the method of integration by parts. 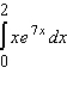
(Multiple Choice)
4.8/5  (32)
(32)
The life span (in years) of a certain brand of color television tube is a continuous random variable with probability density function 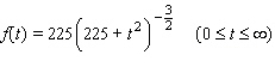 How long is one of these color television tubes expected to last?
How long is one of these color television tubes expected to last?
(Multiple Choice)
4.8/5  (40)
(40)
The velocity of a dragster t seconds after leaving the starting line is 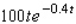 ft/sec. What is the distance covered by the dragster in the first 12 seconds of its run? Round the answer to the nearest whole number.
ft/sec. What is the distance covered by the dragster in the first 12 seconds of its run? Round the answer to the nearest whole number.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 101 - 120 of 250
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)