Exam 6: Integer Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis78 Questions
Exam 2: Introduction to Optimization and Linear Programming76 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet93 Questions
Exam 4: Sensitivity Analysis and the Simplex Method76 Questions
Exam 5: Network Modeling92 Questions
Exam 6: Integer Linear Programming102 Questions
Exam 7: Goal Programming and Multiple Objective Optimization81 Questions
Exam 8: Nonlinear Programming Evolutionary Optimization87 Questions
Exam 9: Regression Analysis93 Questions
Exam 10: Data Mining125 Questions
Exam 11: Time Series Forecasting125 Questions
Exam 12: Introduction to Simulation Using Analytic Solver Platform85 Questions
Exam 13: Queuing Theory97 Questions
Exam 14: Decision Analysis125 Questions
Exam 15: Project Management Online82 Questions
Select questions type
A city wants to locate 2 new fire fighting ladder trucks to maximize the number of tall buildings which they can cover within a 3 minute response time. The city is divided into 4 zones. The fire chief wants to locate no more than one of the trucks in either Zone 1 or Zone 2. The number of tall buildings in each zone and the travel time between zones is listed below. 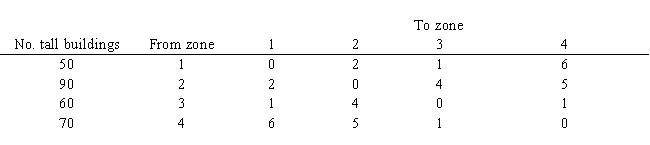
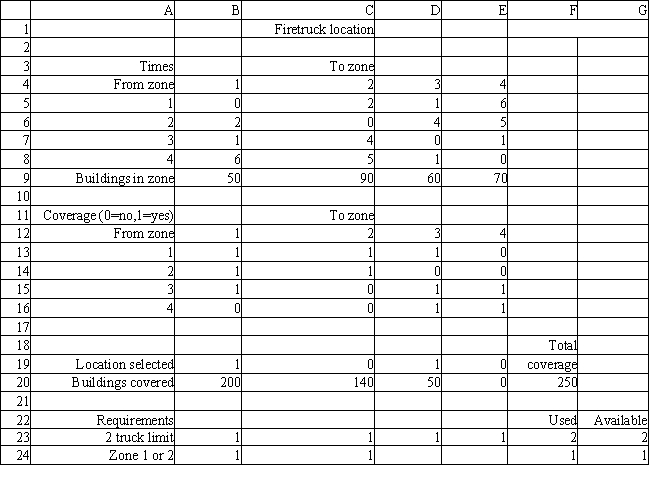
Based on this ILP formulation of the problem what formulas should go in cells B13:B16, B20:E20, F20, and F23:F24 of the following Excel spreadsheet?
Let Xi = 1 if truck located in zone i, 0 otherwise
Based on this ILP formulation of the problem what formulas should go in cells B13:B16, B20:E20, F20, and F23:F24 of the following Excel spreadsheet?
Let Xi = 1 if truck located in zone i, 0 otherwise 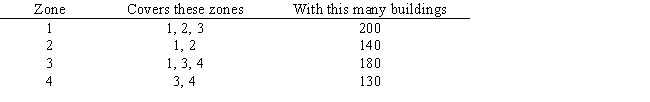
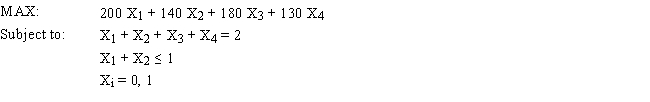
(Essay)
4.8/5  (43)
(43)
A problem in which some decision variables are restricted to assuming only integer values is called a 0-1 programming problem.
(True/False)
4.9/5  (43)
(43)
How are binary variables specified in the Analytic Solver Platform (ASP)?
(Multiple Choice)
4.7/5  (28)
(28)
A cellular phone company wants to locate two new communications towers to cover 4 regions. The company wants to minimize the cost of installing the two towers. The regions that can be covered by each tower site are indicated by a 1 in the following table:  Formulate the ILP for this problem.
Formulate the ILP for this problem.
(Essay)
4.9/5  (32)
(32)
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table.  The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
Formulate the ILP for this problem capturing the ship choice of ports and the supply-to-demand transportation from the ports to the destinations.
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
Formulate the ILP for this problem capturing the ship choice of ports and the supply-to-demand transportation from the ports to the destinations.
(Essay)
4.8/5  (30)
(30)
Consider the constraint
X3 + X4 + X5 + X6 + X7 ≥ 27
Representing Air Express' Monday minimum worker requirement. Why was a "≥" used versus an "="?
(Multiple Choice)
4.7/5  (45)
(45)
A wedding caterer has several wine shops from which it can order champagne. The caterer needs 100 bottles of champagne on a particular weekend for 2 weddings. The first supplier can supply either 40 bottles or 90 bottles.
The relevant decision variable is defined as
X1 = the number of bottles supplied by supplier 1
Which set of constraints reflects the fact that supplier 1 can supply only 40 or 90 bottles?
(Multiple Choice)
4.8/5  (40)
(40)
For maximization problems, the optimal objective function value to the LP relaxation provides what for the optimal objective function value of the ILP problem?
(Multiple Choice)
4.9/5  (38)
(38)
Exhibit 6.2
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table.  The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem. 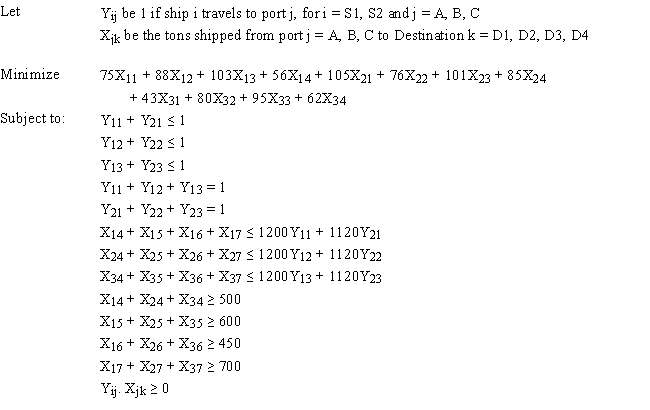
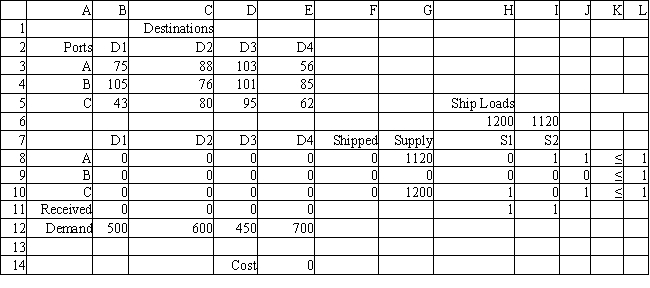 -Refer to Exhibit 6.2. What formula would go into cells G8:G10?
-Refer to Exhibit 6.2. What formula would go into cells G8:G10?
(Essay)
4.8/5  (37)
(37)
How are general integrality requirements indicated in the Analytic Solver Platform?
(Multiple Choice)
4.9/5  (32)
(32)
One approach to solving integer programming problems is to ignore the integrality conditions and solve the problem with continuous decision variables. This is referred to as
(Multiple Choice)
4.9/5  (37)
(37)
Exhibit 6.2
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table.  The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem. 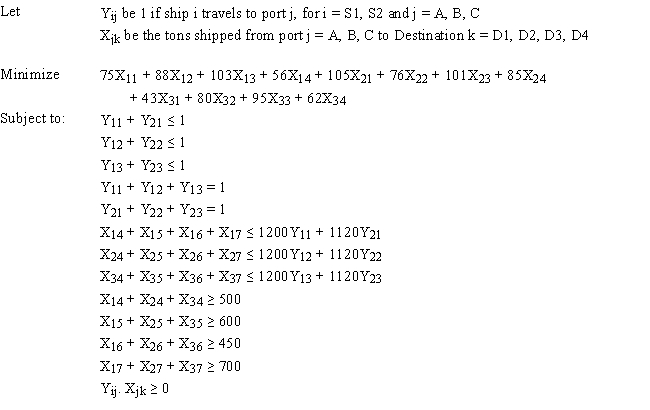
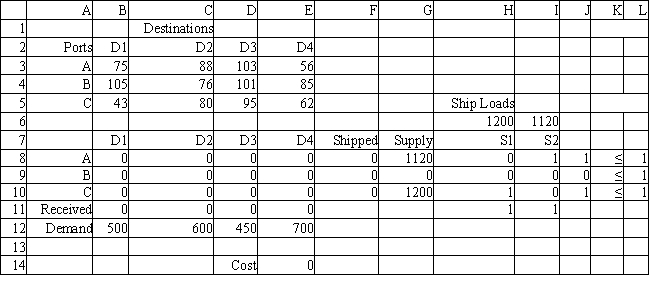 -Refer to Exhibit 6.2. What formula would go into cells B11:E11 and cells F8:F10?
-Refer to Exhibit 6.2. What formula would go into cells B11:E11 and cells F8:F10?
(Essay)
4.8/5  (41)
(41)
A company will be able to obtain a quantity discount on component parts for its three products, X1, X2 and X3 if it produces beyond certain limits. To get the X1 discount it must produce more than 50 X1's. It must produce more than 60 X2's for the X2 discount and 70 X3's for the X3 discount. How many binary variables are required in the formulation of this problem?
(Multiple Choice)
4.9/5  (30)
(30)
One way to find an optimal solution to the IP problem is to:
(Multiple Choice)
4.8/5  (26)
(26)
A company produces three products which must be painted, assembled, and inspected. The machinery must be cleaned and adjusted before each batch is produced. They want to maximize their profits for the amount of operating time they have. The unit profit and setup cost per batch are:  The operation time per unit and total operating hours available are:
The operation time per unit and total operating hours available are:  Formulate the ILP for this problem.
Formulate the ILP for this problem.
(Essay)
4.8/5  (33)
(33)
A company is planning next month's production. It has to pay a setup cost to produce a batch of X4's so if it does produce a batch it wants to produce at least 100 units. Which of the following pairs of constraints show the relationship(s) between the setup variable Y4 and the production quantity variable X4?
(Multiple Choice)
4.9/5  (28)
(28)
Showing 81 - 100 of 102
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)