Exam 6: Discrete Probability Distributions

The probability distribution for the number of automobiles lined up at a Lakeside Olds at opening time (7:30 a.m.) for service is: 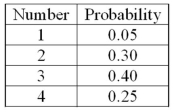On a typical day, how many automobiles should Lakeside Olds expect to be lined up at opening time?

When observing a checkout line at a food store, the average number of people served is 30 per hour. Using the Poisson distribution, what is the probability that no (zero) people check out in any given hour?

The following is a binomial probability distribution with n = 3 and π = 0.20. 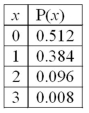The mean of the distribution is _______.

A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. 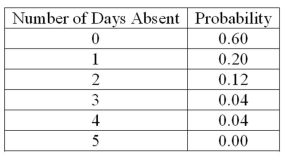What is the mean number of days absent?

A probability distribution shows the distribution of a ______________.

To apply a Poisson probability distribution, the mean can be computed as __________.

In a binomial experiment, the probability of a _________ remains constant.

A new car was put into production. It involved many assembly tasks. Each car was inspected at the end of the assembly line and the number of defects per unit was recorded. For the first 100 cars produced, there were 40 defective cars. Some of the cars had no defects, a few had one defect, and so on. The distribution of defects followed a Poisson distribution. Based on the first 100 cars produced, about how many out of every 1,000 cars assembled should have one or more defects?

The random variable for a Poisson probability distribution can assume an infinite number of values.

In a Poisson distribution, the mean and variance are ________________.

The mean of a binomial distribution is the product of n and π.

Sponsors of a local charity decided to attract wealthy patrons to its $500-a-plate dinner by allowing each patron to buy a set of 20 tickets for the gaming tables. The chance of winning a prize for each of the 20 plays is 50-50. If you bought 20 tickets, what is the chance of winning 15 or more prizes?

A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. 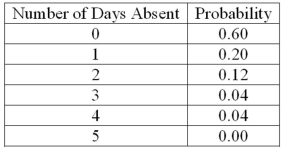Given the probability distribution, which of the following predictions is correct?

A company is studying the number of daily debit card purchases. There were 20 purchases and the probability of a debit card purchase is 0.5. Of the 20 purchases, what is the expected value of the number of debit card purchases?

Which is true for a binomial distribution?

A continuous random variable can assume one of a(n) ____________ number of values within a specific range.

For the following probability distribution: 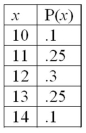The standard deviation is _____________.

In a binomial experiment, the probability of a failure equals _________.

A statistics professor receives an average of five e-mail messages per day from students. Assume the number of messages approximates a Poisson distribution. What is the probability that on a randomly selected day she will have no messages?

There are 10 flights from Minneapolis to St. Cloud each day. The probability that any one flight is late is 0.05. Using the binomial probability formula, what is the probability that none are late?