Exam 15: Oscillations
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vector37 Questions
Exam 4: Motion in Two and Three Dimensions56 Questions
Exam 5: Force and Motion I73 Questions
Exam 6: Force and Motion II74 Questions
Exam 7: Kinetic Energy and Work73 Questions
Exam 8: Potential Energy and Conservation of Energy63 Questions
Exam 9: Center of Mass and Linear Momentum99 Questions
Exam 10: Rotation102 Questions
Exam 11: Rolling, Torque, and Angular Momentum66 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids88 Questions
Exam 15: Oscillations75 Questions
Exam 16: Waves I82 Questions
Exam 17: Waves II71 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases113 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Electric Charge52 Questions
Exam 22: Electric Fields55 Questions
Exam 23: Gauss Law38 Questions
Exam 24: Electric Potential52 Questions
Exam 25: Capacitance61 Questions
Exam 26: Current and Resistance55 Questions
Exam 27: Circuits73 Questions
Exam 28: Magnetic Fields55 Questions
Exam 29: Magnetic Fields Due to Currents49 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current88 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves83 Questions
Exam 34: Images79 Questions
Exam 35: Interference46 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity68 Questions
Exam 38: Photons and Matter Waves57 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms79 Questions
Exam 41: Conduction of Electricity in Solids51 Questions
Exam 42: Nuclear Physics68 Questions
Exam 43: Energy From the Nucleus50 Questions
Exam 44: Quarks, Leptons, and the Big Bang55 Questions
Select questions type
A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the system has an energy of 6.0 J, then the maximum speed of the block is:
(Multiple Choice)
4.8/5  (29)
(29)
Three physical pendulums, with masses m1, m2 = 2m1, and m3 = 3m1, have the same shape and size and are suspended at the same point. Rank them according to their periods, from shortest to longest.
(Multiple Choice)
4.9/5  (29)
(29)
A simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its mid-point. The period then becomes:
(Multiple Choice)
4.8/5  (36)
(36)
Five hoops are each pivoted at a point on the rim and allowed to swing as physical pendulums. The masses and radii are 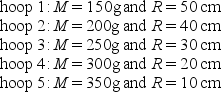 Order the hoops according to the periods of their motions, smallest to largest.
Order the hoops according to the periods of their motions, smallest to largest.
(Multiple Choice)
4.7/5  (36)
(36)
The amplitude and phase constant of an oscillator are determined by:
(Multiple Choice)
4.8/5  (41)
(41)
A simple pendulum consists of a small ball tied to a string and set in oscillation. As the pendulum swings the tension in the string is:
(Multiple Choice)
4.7/5  (39)
(39)
A 3-kg block, attached to a spring, executes simple harmonic motion according to x = 2cos(50t) where x is in meters and t is in seconds. The spring constant of the spring is:
(Multiple Choice)
4.7/5  (23)
(23)
The period of a simple pendulum is 1 s on Earth. When brought to a planet where g is one-tenth that on Earth, its period becomes:
(Multiple Choice)
4.9/5  (34)
(34)
Let U be the potential energy (with the zero at zero displacement) and K be the kinetic energy of a simple harmonic oscillator. Uavg and Kavg are the average values over a cycle. Then:
(Multiple Choice)
4.9/5  (30)
(30)
A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. When it is at x = x1, its kinetic energy is K = 5 J and its potential energy (measured with U = 0 at x = 0) is U = 3 J. When it is at x = -1/2 xm, its total energy is:
(Multiple Choice)
4.8/5  (34)
(34)
The rotational inertia of a uniform thin rod about its end is ML2/3, where M is the mass and L is the length. Such a rod is hung vertically from one end and set into small amplitude oscillation. If L = 1.0 m this rod will have the same period as a simple pendulum of length:
(Multiple Choice)
4.8/5  (35)
(35)
A block on a spring is subjected to an applied sinusoidal force AND to a damping force that is proportional to its velocity. The energy dissipated by damping is supplied by:
(Multiple Choice)
4.9/5  (34)
(34)
A 1.2-kg mass is oscillating without friction on a spring whose spring constant is 3400 N/m. When the mass's displacement is 7.2 cm, what is its acceleration?
(Multiple Choice)
4.8/5  (35)
(35)
If the length of a simple pendulum is doubled, its period will:
(Multiple Choice)
4.8/5  (36)
(36)
In simple harmonic motion, the magnitude of the acceleration is:
(Multiple Choice)
4.9/5  (33)
(33)
Which of the following is NOT required for a simple pendulum undergoing simple harmonic oscillation?
(Multiple Choice)
4.9/5  (33)
(33)
Two identical undamped oscillators have the same amplitude of oscillation only if:
(Multiple Choice)
4.9/5  (37)
(37)
In simple harmonic motion, the magnitude of the acceleration is greatest when:
(Multiple Choice)
4.8/5  (33)
(33)
A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. When it is at x = x1, its kinetic energy is K = 5 J and its potential energy (measured with U = 0 at x = 0) is U = 3 J. When its potential energy is 8 J, it is at:
(Multiple Choice)
4.8/5  (37)
(37)
Both the x and y coordinates of a point execute simple harmonic motion. The frequencies are the same but the amplitudes are different. The resulting orbit might be:
(Multiple Choice)
4.9/5  (35)
(35)
Showing 21 - 40 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)