Exam 10: Rotation
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vectors43 Questions
Exam 4: Motion in Two and Three Dimensions56 Questions
Exam 5: Force and Motion73 Questions
Exam 6: Force and Motion74 Questions
Exam 7: Kinetic Energy and Work73 Questions
Exam 8: Potential Energy and Conservation of Energy65 Questions
Exam 9: Center of Mass and Linear Momentum99 Questions
Exam 10: Rotation102 Questions
Exam 11: Rolling, Torque, and Angular Momentum67 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation61 Questions
Exam 14: Fluids91 Questions
Exam 15: Oscillations80 Questions
Exam 16: Waves83 Questions
Exam 17: Waves72 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases114 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Coulombs Law52 Questions
Exam 22: Electric Fields55 Questions
Exam 23: Gauss Law44 Questions
Exam 24: Electric Potential55 Questions
Exam 25: Capacitance61 Questions
Exam 26: Current and Resistance55 Questions
Exam 27: Circuits75 Questions
Exam 28: Magnetic Fields53 Questions
Exam 29: Magnetic Fields Due to Currents49 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current89 Questions
Exam 32: Maxwells Equations; Magnetism of Matter87 Questions
Exam 33: Electromagnetic Waves83 Questions
Exam 34: Images79 Questions
Exam 35: Interference 147 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity69 Questions
Exam 38: Photons and Matter Waves59 Questions
Exam 39: More About Matter Waves45 Questions
Exam 40: All About Atoms79 Questions
Exam 41: Conduction of Electricity in Solids51 Questions
Exam 42: Energy From the Nucleus50 Questions
Exam 43: Quarks, Leptons, and the Big Bang59 Questions
Select questions type
A wheel starts from rest and spins with a constant angular acceleration.As time goes on the acceleration vector for a point on the rim:
(Multiple Choice)
4.9/5  (38)
(38)
To increase the rotational inertia of a solid disk about its axis without changing its mass:
(Multiple Choice)
4.7/5  (35)
(35)
String is wrapped around the periphery of a 5.0-cm radius cylinder, free to rotate on its axis.The string is pulled straight out at a constant rate of 10 cm/s and does not slip on the cylinder.As each small segment of string leaves the cylinder, the segment's acceleration changes by:
(Multiple Choice)
4.7/5  (45)
(45)
This graph shows the angular velocity of a turntable as a function of time.What is its average angular acceleration between t = 2 s and t = 4 s? 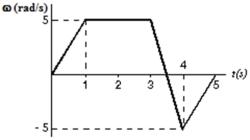
(Multiple Choice)
4.7/5  (43)
(43)
A wheel is spinning at 27 rad/s but is slowing with an angular acceleration that has a magnitude given by (3.0 rad/s4)t2. It stops in a time of:
(Multiple Choice)
4.8/5  (42)
(42)
A particle moves in a circular path of radius 0.10 m with a constant angular speed of 5 rev/s.The acceleration of the particle is:
(Multiple Choice)
4.8/5  (43)
(43)
A wheel starts from rest and has an angular acceleration that is given by (t)= 6 rad/s4)t2.The angle through which it turns in time t is given by:
(Multiple Choice)
4.9/5  (44)
(44)
A uniform solid cylinder made of lead has the same mass and the same length as a uniform solid cylinder made of wood.The rotational inertia of the lead cylinder compared to the wooden one is:
(Multiple Choice)
4.8/5  (33)
(33)
A pulley with a radius of 3.0 cm and a rotational inertia of 4.5 *10-3 kg.m2 is suspended from the ceiling.A rope passes over it with a 2.0-kg block attached to one end and a 4.0-kg block attached to the other.The rope does not slip on the pulley.At any instant after the blocks start moving the object with the greatest kinetic energy is:
(Multiple Choice)
4.8/5  (40)
(40)
The coordinate of an object is given as a function of time by θ = 7t - 3t2, where θ is in radians and t is in seconds.Its average velocity over the interval from t = 0 to t = 2 s is:
(Multiple Choice)
4.9/5  (40)
(40)
The meter stick shown below rotates about an axis through the point marked  , 20 cm from one end.Five forces act on the stick: one at each end, one at the pivot point, and two 40 cm from one end, as shown.The magnitudes of the forces are all the same.Rank the forces according to the magnitudes of the torques they produce about the pivot point, least to greatest.
, 20 cm from one end.Five forces act on the stick: one at each end, one at the pivot point, and two 40 cm from one end, as shown.The magnitudes of the forces are all the same.Rank the forces according to the magnitudes of the torques they produce about the pivot point, least to greatest. 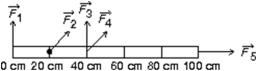
(Multiple Choice)
5.0/5  (38)
(38)
An object rotates from θ1 to θ2 through an angle that is less than 2π radians.Which of the following represents its angular displacement?
(Multiple Choice)
4.8/5  (30)
(30)
A thin rod of length L has a density that increases along its length, ρ = ρ0x.What is the rotational inertia of the rod around its less dense end?
(Multiple Choice)
4.7/5  (30)
(30)
When a thin uniform stick of mass M and length L is pivoted about its midpoint, its rotational inertia is ML2/12.When pivoted about a parallel axis through one end, its rotational inertia is:
(Multiple Choice)
4.7/5  (28)
(28)
The rotational inertia of a solid uniform sphere about a diameter is (2/5)MR2, where M is its mass and R is its radius.If the sphere is pivoted about an axis that is tangent to its surface, its rotational inertia is:
(Multiple Choice)
4.8/5  (37)
(37)
A flywheel of diameter 1.2 m has a constant angular acceleration of 5.0 rad/s2.The tangential acceleration of a point on its rim is:
(Multiple Choice)
4.8/5  (40)
(40)
A child, riding on a large merry-go-round, travels a distance of 3000 m in a circle of diameter 40 m.The total angle through which she revolves is:
(Multiple Choice)
4.9/5  (37)
(37)
A car travels north at constant velocity.It goes over a piece of mud which sticks to the tire.The initial acceleration of the mud, as it leaves the ground, is:
(Multiple Choice)
4.8/5  (40)
(40)
Showing 41 - 60 of 102
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)