Exam 5: Integer Programming

Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision. The table below shows the cost ($ per item) for shipping from each DC to each region. Region 1 1 3 3 2 2 2 4 1 3 3 3 2 2 3 The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units. Assume that Xij = quantity shipped from distribution i to region j. i = 1,2,3 and j = 1, 2, 3, 4. Assume that Yi = 0 or 1 where i = distribution center 1, 2 or 3. -The constraint for distribution center 1 is:

Future Plastics manufactures plastic products for industrial use worldwide. In order to meet demand, they are considering setting up a facility in each region in order to lower transportation cost and to possibly avoid duties that could be imposed if the product is imported from another region. The disadvantage of this approach is that plants are sized to meet local demand and may not fully exploit economies of scale. Therefore, Future Plastics is also interested in determining the appropriate size of the facility to build in each location and are choosing between facilities with capacities of 5 or 10 million. The fixed costs of each facility as well as the cost of shipping between regions is shown in the table below. The decision variables are defined as follows: Xij = quantity shipped from supply region i to demand region j. i = 1, 2, 3, 4 and j = 1, 2, 3, 4. Yik = 1 if facility k is selected for supply region i; 0 otherwise, where i = 1, 2, 3, 4 for each supply region; k = 1 (low capacity facility) or 2 (high capacity facility) 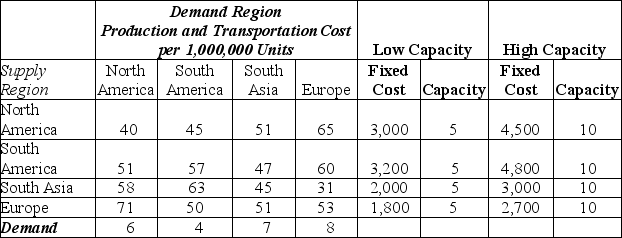-The constraint for the South Asia demand region is:

Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision. The table below shows the cost ($ per item) for shipping from each DC to each region. Region 1 1 3 3 2 2 2 4 1 3 3 3 2 2 3 The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units. Assume that Xij = quantity shipped from distribution i to region j. i = 1,2,3 and j = 1, 2, 3, 4. Assume that Yi = 0 or 1 where i = distribution center 1, 2 or 3. -You have been asked to select at least 3 out of 7 possible sites for oil exploration. Designate each site as S1, S2, S3, S4, S5, S6, and S7. The restrictions are: Restriction 1. Evaluating sites S1 and S3 will prevent you from exploring site S7. Restriction 2. Evaluating sites S2 or S4 will prevent you from assessing site S5. Restriction 3. Of all the sites, at least 3 should be assessed. Assuming that Si is a binary variable, write the constraint(s) for the second restriction.

The branch and bound method can only be used for maximization integer programming problems.

If we are solving a 0-1 integer programming problem, the constraint x1 + x2 ≤ 1 is a ________ constraint.

If we are solving a 0-1 integer programming problem, the constraint x1 + x2 ≤ 1 is a mutually exclusive constraint.

Consider the following integer linear programming problem: Max Z= 3+2 Subject to: 3+5\leq30 4+2\leq28 \leq8 ,\geq0 and integer The solution to the linear programming formulation is: x1 = 5.714, x2 = 2.571. What is the optimal solution to the integer linear programming problem? State the optimal values of decision variables and the value of the objective function.

You have been asked to select at least 3 out of 7 possible sites for oil exploration. Designate each site as S1, S2, S3, S4, S5, S6, and S7. The restrictions are: Restriction 1. Evaluating sites S1 and S3 will prevent you from exploring site S7. Restriction 2. Evaluating sites S2 or S4 will prevent you from assessing site S5. Restriction 3. Of all the sites, at least 3 should be assessed. Assuming that Si is a binary variable, write the constraint for the first restriction.

A ________ integer model allows for the possibility that some decision variables are not integers.

In an integer program, if building one facility required the construction of another type of facility, this would be written as: ________.

If we are solving a 0-1 integer programming problem, the constraint x1 + x2 ≤ 1 is a ________ constraint.

If a maximization linear programming problem consists of all less-than-or-equal-to constraints with all positive coefficients and the objective function consists of all positive objective function coefficients, then rounding down the linear programming optimal solution values of the decision variables will ________ result in a(n) ________ solution to the integer linear programming problem.

If one location for a warehouse can be selected only if a specific location for a manufacturing facility is also selected, this decision can be represented by a ________ constraint.

If we are solving a 0-1 integer programming problem, the constraint x1 + x2 = 1 is a mutually exclusive constraint.

If we are solving a 0-1 integer programming problem, the constraint x1 + x2 + x3 ≤ 3 is a mutually exclusive constraint.

The management scientist's fiance informed him that if they were to be married, he would also have to welcome her mother into their home. The management scientist should model this decision as a contingency constraint.

Saba conducts regular tours of his favorite city in the world, Paris. Each semester he selects among the finest students in the university and escorts them to the City of Lights. In addition to a world-class education on conducting business in Europe, he arranges a number of cultural outings for them to help them immerse themselves in all that France has to offer. He collects an extra $100 from each student for this purpose and limits his tour group to ten lucky individuals. Some of the events (and their prices) he proposes to the students include: Eiffel Tower visit, $40 per student, E Paris Sewer spelunking, $20 per student, S Half day passes to the Louvre, $60 per student, L Bon Beret tour, $50 per student, B So much to do and so little time! -What would the constraints be if the Eiffel Tower visit needed to take place at the same time as the half day at the Louvre and if students taking the Paris Sewer tour had to wear the special sanitary beret available only from the Bon Beret tour?

In a mixed integer model, some solution values for decision variables are integer and others can be non-integer.

Solve the following integer linear program graphically. MAX Z = 5x1 + 8x2 s.t. x1 + x2 ? 6    5x1 + 9x2 ? 45    x1, x2 ? 0 and integer

Saba conducts regular tours of his favorite city in the world, Paris. Each semester he selects among the finest students in the university and escorts them to the City of Lights. In addition to a world-class education on conducting business in Europe, he arranges a number of cultural outings for them to help them immerse themselves in all that France has to offer. He collects an extra $100 from each student for this purpose and limits his tour group to ten lucky individuals. Some of the events (and their prices) he proposes to the students include: Eiffel Tower visit, $40 per student, E Paris Sewer spelunking, $20 per student, S Half day passes to the Louvre, $60 per student, L Bon Beret tour, $50 per student, B So much to do and so little time! -If we are solving a 0-1 integer programming problem, the constraint x1 ≤ x2 is a ________ constraint.