Exam 5: Integer Programming

In a 0-1 integer model, the solution values of the decision variables are 0 or 1.

In an integer program, if we were choosing between two locations to build a facility, this would be written as: ________.

You have been asked to select at least 3 out of 7 possible sites for oil exploration. Designate each site as S1, S2, S3, S4, S5, S6, and S7. The restrictions are: Restriction 1. Evaluating sites S1 and S3 will prevent you from exploring site S7. Restriction 2. Evaluating sites S2 or S4 will prevent you from assessing site S5. Restriction 3. Of all the sites, at least 3 should be assessed. Assuming that Si is a binary variable, the constraint for the first restriction is :

Rounding non-integer solution values up to the nearest integer value will still result in a feasible solution.

Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision. The table below shows the cost ($ per item) for shipping from each DC to each region. Region 1 1 3 3 2 2 2 4 1 3 3 3 2 2 3 The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units. -Write the constraints for the three distribution centers.

Max Z = 3x1 + 5x2 Subject to: 7x1 + 12x2 ? 136        3x1 + 5x2 ? 36        x1, x2 ? 0 and integer Find the optimal solution.

If we are solving a 0-1 integer programming problem, the constraint x1 ≤ x2 is a ________ constraint.

Due to increased sales, a company is considering building three new distribution centers (DCs) to serve four regional sales areas. The annual cost to operate DC 1 is $500 (in thousands of dollars). The cost to operate DC 2 is $600 (in thousands of dollars.). The cost to operate DC 3 is $525 (in thousands of dollars). Assume that the variable cost of operating at each location is the same, and therefore not a consideration in making the location decision. The table below shows the cost ($ per item) for shipping from each DC to each region. Region 1 1 3 3 2 2 2 4 1 3 3 3 2 2 3 The demand for region A is 70,000 units; for region B, 100,000 units; for region C, 50,000 units; and for region D, 80,000 units. Assume that the minimum capacity for the distribution center will be 500,000 units. -Write the objective function for this problem.

In formulating a mixed integer programming problem, the constraint x1 + x2 ≤ 500y1 where y1 is a 0-1 variable and x1 and x2 are continuous variables, then x1 + x2 = 500 if y1 is ________.

The Exorbitant Course Fees. The $75 per credit hour course fee tacked on to all the MBA classes has generated a windfall of $56,250 in its first semester. "Now we just need to make sure we spend it all," the Assistant Dean cackled. She charged the Graduate Curriculum Committee with generating a shopping list before their next meeting. Four months later, the chairman of the committee distributed the following. As the professor for the quantitative modeling course, he tended to think in terms of decision variables, so he added the left-most column for ease of use. Decision Variable Item Cost Note A iPads for everybody \ 750/ unit Must get a cover if these are purchased B iPad covers with MBA logo \ 25/ unit Not needed unless we buy iPads C Speaker series \ 15,000 Can't afford both this and the iPads D Subscriptions to the Wall Street Joumal \ 10/ unit Don't need if we have the electronic version Subscriptions to the electronic version of the Wall E Street Joumal \5 /unit Worthless without the iPads -Which constraint best describes the situation with decision variables A and B?

The Exorbitant Course Fees. The $75 per credit hour course fee tacked on to all the MBA classes has generated a windfall of $56,250 in its first semester. "Now we just need to make sure we spend it all," the Assistant Dean cackled. She charged the Graduate Curriculum Committee with generating a shopping list before their next meeting. Four months later, the chairman of the committee distributed the following. As the professor for the quantitative modeling course, he tended to think in terms of decision variables, so he added the left-most column for ease of use. Decision Variable Item Cost Note A iPads for everybody \ 750/ unit Must get a cover if these are purchased B iPad covers with MBA logo \ 25/ unit Not needed unless we buy iPads C Speaker series \ 15,000 Can't afford both this and the iPads D Subscriptions to the Wall Street Joumal \ 10/ unit Don't need if we have the electronic version Subscriptions to the electronic version of the Wall E Street Joumal \5 /unit Worthless without the iPads -Which of these formulations of the budget constraint is correct? Assume that there are 20 students in this semesters MBA class.

The branch and bound solution method cannot be applied to 0-1 integer programming problems.

The Wiethoff Company has a contract to produce 10,000 garden hoses for a customer. Wiethoff has four different machines that can produce this kind of hose. Because these machines are from different manufacturers and use differing technologies, their specifications are not the same. Machine Fixed Cost to Setup Production Run Variable Cost per Hose Capacity 1 750 1.25 6000 2 500 1.50 7500 3 1000 1.00 4000 4 300 2.00 5000 -This problem requires two different kinds of decision variables. Clearly define each kind.

________ variables are best suited to be the decision variables when dealing with yes-or-no decisions.

Consider a capital budgeting example with five projects from which to select. Let x1 = 1 if project a is selected, 0 if not, for a = 1, 2, 3, 4, 5. Projects cost $100, $200, $150, $75, and $300, respectively. The budget is $450. -Write the appropriate constraint for the following condition: Choose no fewer than 3 projects.

The Wiethoff Company has a contract to produce 10,000 garden hoses for a customer. Wiethoff has four different machines that can produce this kind of hose. Because these machines are from different manufacturers and use differing technologies, their specifications are not the same. Machine Fixed Cost to Setup Production Run Variable Cost per Hose Capacity 1 750 1.25 6000 2 500 1.50 7500 3 1000 1.00 4000 4 300 2.00 5000 -Write a constraint that will ensure that Weithoff purchases exactly two machines.

Future Plastics manufactures plastic products for industrial use worldwide. In order to meet demand, they are considering setting up a facility in each region in order to lower transportation cost and to possibly avoid duties that could be imposed if the product is imported from another region. The disadvantage of this approach is that plants are sized to meet local demand and may not fully exploit economies of scale. Therefore, Future Plastics is also interested in determining the appropriate size of the facility to build in each location and are choosing between facilities with capacities of 5 or 10 million. The fixed costs of each facility as well as the cost of shipping between regions is shown in the table below. The decision variables are defined as follows: Xij = quantity shipped from supply region i to demand region j. i = 1, 2, 3, 4 and j = 1, 2, 3, 4. Yik = 1 if facility k is selected for supply region i; 0 otherwise, where i = 1, 2, 3, 4 for each supply region; k = 1 (low capacity facility) or 2 (high capacity facility) 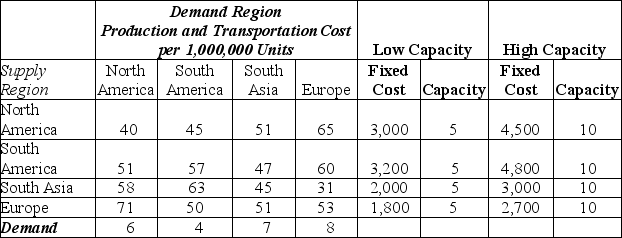-Which of these constraints will ensure that either a low capacity or a high facility capacity facility is built in the European supply region?

In a 0-1 integer programming model, if the constraint x1 - x2 = 0, it means when project 1 is selected, project 2 ________ be selected.

...............

In a problem involving capital budgeting applications, the 0-1 variables designate the acceptance or rejection of the different projects.