Exam 7: Probability
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine whether the given events A and B are independent. 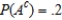 ,
, 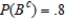 , and
, and 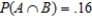 . Answer dependent or independent.
. Answer dependent or independent.
Free
(Short Answer)
4.9/5  (28)
(28)
Correct Answer:
independent
An experiment in which the three mutually exclusive events, A, B, and C form a partition of the uniform sample space S is depicted in the diagram. 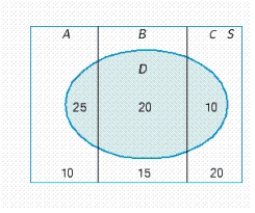 Find P(Dc) and P(B|Dc).
If necessary, round your answer to two decimal places.
P(Dc) = __________
P(B|Dc) = __________
Find P(Dc) and P(B|Dc).
If necessary, round your answer to two decimal places.
P(Dc) = __________
P(B|Dc) = __________
Free
(Short Answer)
4.8/5  (30)
(30)
Correct Answer:
0.45; 0.33
Based on data obtained from the National Institute of Dental Research, it has been determined that 44% of 12-year-olds have never had a cavity, 35% of 13-year-olds have never had a cavity, and 25% of 14-year-olds have never had a cavity. If a child is selected at random from a group of 20 junior high school students comprising four 12-year-olds, six 13-year-olds, and ten 14-year-olds and this child does not have a cavity, what is the probability that this child is 14 years old?
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
C
An insurance company has compiled the accompanying data relating the age of drivers and the accident rate (the probability of being involved in an accident during a 1-year period) for drivers within that group:  a. What is the probability that an insured driver will be involved in an accident during a particular 1-year period? If necessary, round your answer to two decimal places.
__________
b. What is the probability that an insured driver who is involved in an accident is under 25? If necessary, round your answer to two decimal places.
__________
a. What is the probability that an insured driver will be involved in an accident during a particular 1-year period? If necessary, round your answer to two decimal places.
__________
b. What is the probability that an insured driver who is involved in an accident is under 25? If necessary, round your answer to two decimal places.
__________
(Essay)
4.9/5  (47)
(47)
Let 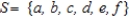 be a sample space of an experiment and let
be a sample space of an experiment and let 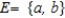 , and
, and 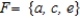 be events of this experiment.
Find the events E ∪ F and E ∩ F.
be events of this experiment.
Find the events E ∪ F and E ∩ F.
(Multiple Choice)
4.7/5  (27)
(27)
Let S be any sample space and N, F, and E be any three events associated with the experiment. Describe the following event, using the symbols ∪, ∩, and c.
The event that E does not occur.
(Multiple Choice)
4.8/5  (36)
(36)
An experiment consists of casting a pair of dice and observing the number that falls uppermost on each die. We may represent each outcome of the experiment by an ordered pair of numbers, the first representing the number that appears uppermost on the first die and the second representing the number that appears uppermost on the second die. Consider the sample space S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Determine the event that the sum of the numbers falling uppermost is greater than or equal to 7.
(Multiple Choice)
4.9/5  (44)
(44)
An experiment consists of selecting a card at random from a 52-card deck. Find the probability of the event that a club or a queen is drawn. Give the answer as a fraction.
(Essay)
4.9/5  (41)
(41)
Eight players, A, B, C, D, E, F, G, and H, are competing in a series of elimination matches of a tennis tournament in which the winner of each preliminary match will advance to the semifinals and the winner of the semifinals will advance to the finals. An outline of the scheduled matches follows. Describe a sample space listing the possible participants in the finals. 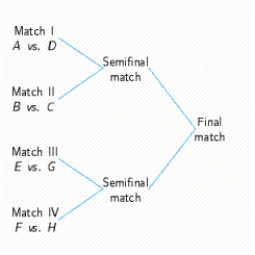
(Multiple Choice)
4.8/5  (31)
(31)
Let S = {s1, s2, s3, s4, s5, s6} be the sample space associated with an experiment having the following probability distribution: 
Find the probability of the event A = {s1, s3}.
Find the probability of the event A = {s1, s3}.
(Essay)
4.8/5  (37)
(37)
An experiment in which the three mutually exclusive events, A, B, and C form a partition of the uniform sample space S is depicted in the diagram. 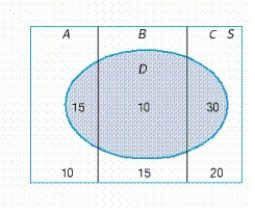
Find
Find 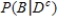 .
.
(Multiple Choice)
4.8/5  (40)
(40)
Urn A contains eight white and four black balls. Urn B contains seven white and three black balls. A ball is drawn from urn A and then transferred to urn B. A ball is then drawn from urn B. What is the probability that the transferred ball was black given that the second ball drawn was white?
(Multiple Choice)
4.8/5  (49)
(49)
An experiment consists of tossing a coin, rolling a die, and observing the outcomes. Describe the event "A head is tossed and an even number is rolled."
(Multiple Choice)
4.8/5  (30)
(30)
Let 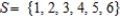 ,
, 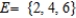 ,
, 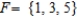 and
and 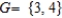 .
Find the event E ∪ F ∪ G.
Express your answer using set notation.
.
Find the event E ∪ F ∪ G.
Express your answer using set notation.
(Essay)
4.8/5  (37)
(37)
Two light bulbs are selected at random from a lot of 26, of which 4 are defective. What is the probability that at least 1 of the light bulbs is defective?
(Multiple Choice)
4.9/5  (34)
(34)
A pair of dice is cast, and the number that appears uppermost on each die is observed. Find the probability of the event that one die shows a 6, and the other is a number less than 4.
(Multiple Choice)
4.9/5  (40)
(40)
An experiment consists of casting a pair of dice and observing the number that falls uppermost on each die. We may represent each outcome of the experiment by an ordered pair of numbers, the first representing the number that appears uppermost on the first die and the second representing the number that appears uppermost on the second die. Consider the sample space S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Determine the event that the number falling uppermost on one die is a 4 and the number falling uppermost on the other die is less than 4.
(Multiple Choice)
4.9/5  (39)
(39)
Two cards are drawn in succession without replacement from a standard deck of 52 cards. What is the probability that the first card is a heart given that the second card is a clubs?
(Multiple Choice)
4.9/5  (41)
(41)
An experiment in which the three mutually exclusive events, A, B, and C form a partition of the uniform sample space S is depicted in the diagram.
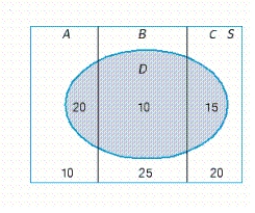
Find P(Dc) and P(B|Dc).
If necessary, round your answer to two decimal places.
P(Dc) = __________
P(B|Dc) = __________
Find P(Dc) and P(B|Dc).
If necessary, round your answer to two decimal places.
P(Dc) = __________
P(B|Dc) = __________
(Short Answer)
4.9/5  (32)
(32)
An experiment consists of selecting a card at random from a 52-card deck. Find the probability of the event that an ace is not drawn. Give the answer as a fraction.
(Essay)
4.8/5  (25)
(25)
Showing 1 - 20 of 273
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)