Exam 3: Linear Programming: a Geometric Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine graphically the solution set for the system of inequalities. 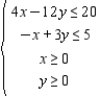
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
D
Find the graphical solution of the inequality. 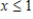
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
A finance company has a total of $15 million earmarked for homeowner and auto loans. On the average, homeowner loans have a 10% annual rate of return, whereas auto loans yield a 12% annual rate of return. Management has also stipulated that the total amount of homeowner loans should be greater than or equal to 4 times the total amount of automobile loans. Determine the total amount of loans of each type the company should extend to each category in order to maximize its returns.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
Solve the linear programming problem by the method of corners. Maximize 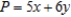 subject to
subject to 
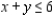
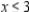
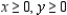
(Multiple Choice)
4.9/5  (37)
(37)
Formulate but do not solve the following exercise as a linear programming problem. A farmer has 140 acres of land suitable for cultivating crops A and B. The cost of cultivating crop A is $30/acre, whereas that of crop B is $80/acre. The farmer has a maximum of $5,700 available for land cultivation. Each acre of crop A requires 30 labor-hours, and each acre of crop B requires 35 labor-hours. The farmer has a maximum of 4,800 labor-hours available. If she expects to make a profit of $130/acre on crop A and $230/acre on crop B, how many acres of each crop should she plant in order to maximize her profit?
(Multiple Choice)
4.9/5  (28)
(28)
Formulate but do not solve the following exercise as a linear programming problem. A financier plans to invest up to $400,000 in two projects. Project A yields a return of 12% on the investment, whereas project B yields a return of 13% on the investment. Because the investment in project B is riskier than the investment in project A, she has decided that the investment in project B should not exceed 45% of the total investment. How much should the financier invest in each project in order to maximize the return on her investment?
(Multiple Choice)
4.9/5  (37)
(37)
A company manufactures two products, A and B, on machines I and II. The company will realize a profit of $3/unit of product A and a profit of $4/unit of product B. Manufacturing 1 unit of product A requires 6 min on machine I and 5 min on machine II. Manufacturing 1 unit of product B requires 9 min on machine I and 4 min on machine II. There are 15 hr of time available on machine I and 9 hr of time available on machine II in each work shift. How many units of each product should be produced in each shift to maximize the company's profit? Find the range of values that the contribution to the profit of 1 unit of product A can assume without changing the optimal solution.
Find the range of values that resource associated with the time constraint on machine I can assume.
Find the shadow price for the resource associated with the time constraint on machine I.
(Multiple Choice)
4.7/5  (28)
(28)
Write a system of linear inequalities that describes the shaded region. 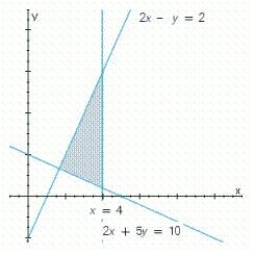
(Multiple Choice)
4.8/5  (32)
(32)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 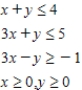
(Multiple Choice)
4.8/5  (46)
(46)
Determine graphically the solution set for the system of inequalities and indicate whether the solution set is bounded or unbounded. 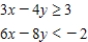
(Multiple Choice)
4.9/5  (35)
(35)
Deluxe River Cruises operates a fleet of river vessels. The fleet has two types of vessels: a type A vessel has 60 deluxe cabins and 160 standard cabins, whereas a type B vessel has 80 deluxe cabins and 120 standard cabins. Under a charter agreement with the Odyssey Travel Agency, Deluxe River Cruises is to provide Odyssey with a minimum of 780 deluxe and 1520 standard cabins for their 20-day cruise in May. It costs $49,000 to operate a type A vessel and $54,000 to operate a type B vessel for that period. How many of each type of vessel should be used to keep the operating costs to a minimum?
(Multiple Choice)
4.8/5  (34)
(34)
Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,000 lb of cast iron and 22 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 200 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits? The range of values that the coefficient of x can assume without changing the optimal solution is 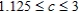 If the contribution to the profit of a model A grate is changed to $1.90/grate, will the original optimal solution still hold? What will be the new optimal solution?
If the contribution to the profit of a model A grate is changed to $1.90/grate, will the original optimal solution still hold? What will be the new optimal solution?
(Multiple Choice)
4.7/5  (37)
(37)
Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 2 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,000 lb of cast iron and 20 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 200 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits?
Use the method of corners to solve the problem. Find the range of values that the coefficient of x can assume without changing the optimal solution. Identify the binding and nonbinding constraints.
(Multiple Choice)
4.7/5  (35)
(35)
As a part of a campaign to promote its annual clearance sale, the Excelsior Company decided to buy television advertising time on Station KAOS. Excelsior's advertising budget is $ 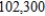 . Morning time costs $
. Morning time costs $ 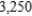 / minute, afternoon time costs $
/ minute, afternoon time costs $ 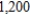 / minute, and evening (prime) time costs $
/ minute, and evening (prime) time costs $ 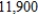 / minute. Because of previous commitments, KAOS cannot offer Excelsior more than
/ minute. Because of previous commitments, KAOS cannot offer Excelsior more than  min of prime time or more than a total of
min of prime time or more than a total of 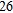 min of advertising time over the 2 weeks in which the commercials are to be run. KAOS estimates that morning commercials are seen by 206,000 people, afternoon commercials are seen by 114,000 people, and evening commercials are seen by 600,000 people. How much morning, afternoon, and evening advertising time should Excelsior buy to maximize exposure of its commercials?
min of advertising time over the 2 weeks in which the commercials are to be run. KAOS estimates that morning commercials are seen by 206,000 people, afternoon commercials are seen by 114,000 people, and evening commercials are seen by 600,000 people. How much morning, afternoon, and evening advertising time should Excelsior buy to maximize exposure of its commercials?
(Multiple Choice)
4.7/5  (30)
(30)
Solve the linear programming problem by the method of corners.
Maximize 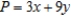 subject to
subject to 
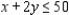
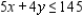
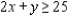
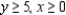 x = __________; y = __________; P = __________
x = __________; y = __________; P = __________
(Essay)
4.9/5  (29)
(29)
Find the optimal (maximum and/or minimum) value(s) of the given objective function on the feasible set S.
Z = 5x  7y
7y
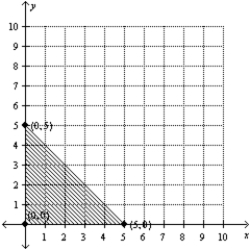
(Multiple Choice)
4.9/5  (40)
(40)
Formulate but do not solve the following exercise as a linear programming problem.
CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates. These juices will be packaged in 2-qt (64 fluid-oz) cartons. To make one carton of pineapple-orange juice requires 7 oz each of pineapple and orange juice concentrates. To make one carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate. Finally, to make one carton of pineapple-orange-banana juice requires 5 oz of pineapple juice concentrate, 6 oz of orange juice concentrate, and 3 oz of banana pulp. The company has decided to allot 16,000 oz of pineapple juice concentrate, 25,000 oz of orange juice concentrate, and 3,000 oz of banana pulp concentrate for the initial production run. The company also stipulated that the production of pineapple-orange-banana juice should not exceed 500 cartons. Its profit on one carton of pineapple-orange juice is $1.10; its profit on one carton of orange-banana juice is $0.90, and its profit on one carton of pineapple-orange-banana juice is $0.80. To realize a maximum profit, how many cartons of each blend should the company produce?
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 214
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)