Exam 9: Markov Chains and the Theory of Games
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine whether the given matrix is stochastic. 
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
A
Determine whether the matrix is regular. 
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
A
Determine whether the given two-person, zero-sum matrix game is strictly determined. 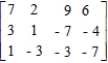
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
B
Determine whether the given two-person, zero-sum matrix game is strictly determined. 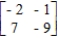
(Multiple Choice)
4.8/5  (36)
(36)
Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. Give your answer to one decimal place, if necessary.
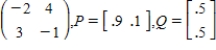
(Short Answer)
4.9/5  (43)
(43)
Determine which of the given matrices is an absorbing stochastic matrix.
(Multiple Choice)
4.9/5  (35)
(35)
Compute the steady-state matrix of the given stochastic matrix. 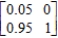
(Multiple Choice)
4.8/5  (33)
(33)
Two dentists, Lydia Russell and Jerry Carlton, are planning to establish practices in a newly developed community. Both have allocated approximately the same total budget for advertising in the local newspaper and for the distribution of fliers announcing their practices. Because of the location of their offices, Russell is expected to get 46% of the business if both dentists advertise only in the local newspaper; if both dentists advertise through fliers, then Russell is expected to get 43% of the business; if Russell advertises exclusively in the local newspaper and Carlton advertises exclusively through fliers, then Russell is expected to get 68% of the business. Finally, if Russell advertises through fliers exclusively and Carlton advertises exclusively in the local newspaper, then Russell is expected to get 50% of the business. Find the optimal strategy for both Russell and Carlton.
(Multiple Choice)
4.8/5  (32)
(32)
Because of the continued successful implementation of an urban renewal program, it is expected that each year 5% of the population currently residing in the city will move to the suburbs and 6% of the population currently residing in the suburbs will move into the city. If the initial probability distribution is
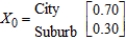
what will be the population distribution of the city after 1 year?
__________ %
After 2 years?
__________ %
Assume that the total population of the metropolitan area remains constant. Round your answers to the nearest thousandth, if necessary.
__________ %
__________ %
what will be the population distribution of the city after 1 year?
__________ %
After 2 years?
__________ %
Assume that the total population of the metropolitan area remains constant. Round your answers to the nearest thousandth, if necessary.
__________ %
__________ %
(Short Answer)
4.8/5  (31)
(31)
Consider the two-person, zero-sum matrix, strictly determined game. 
Find the value of the game.
Find the value of the game.
(Multiple Choice)
4.7/5  (35)
(35)
Find 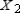 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 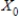 and the given transition matrix
and the given transition matrix 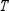 .
.
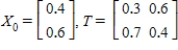
(Essay)
4.8/5  (41)
(41)
A psychologist conducts an experiment in which a mouse is placed in a T-maze, where it has a choice at the T-junction of turning left and receiving a reward (cheese) or turning right and receiving a mild shock. At the end of each trial a record is kept of the mouse's response. It is observed that the mouse is as likely to turn left (state 1) as right (state 2) during the first trial. In subsequent trials, however, the observation is made that if the mouse had turned left in the previous trial, then the probability that it will turn left in the next trial is .6, whereas the probability that it will turn right is .4. If the mouse had turned right in the previous trial, then the probability that it will turn right in the next trial is .2, whereas the probability that it will turn left is .8. In the long run, what percentage of the time will the mouse turn left at the T-junction? Please round the answer to one decimal place.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the given matrix is an absorbing stochastic matrix.

(Short Answer)
4.9/5  (35)
(35)
Find X2 (the probability distribution of the system after two observations) for the given distribution vector X0 and the given transition matrix T.
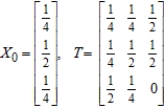
(Essay)
4.8/5  (38)
(38)
The payoff matrix for a game is 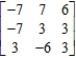 .
Find the expected payoff to the row player if
.
Find the expected payoff to the row player if 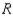 uses the maximin strategy 50% of the time and chooses each of the other two rows 25% of the time, while
uses the maximin strategy 50% of the time and chooses each of the other two rows 25% of the time, while 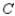 uses the minimax strategy 60% of the time and chooses each of the other columns 20% of the time.
uses the minimax strategy 60% of the time and chooses each of the other columns 20% of the time.
(Multiple Choice)
4.8/5  (33)
(33)
Find the steady-state vector for the transition matrix. 
(Multiple Choice)
4.9/5  (37)
(37)
Find 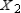 (the probability distribution of the system after two observations) for the given distribution vector
(the probability distribution of the system after two observations) for the given distribution vector 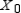 and the given transition matrix
and the given transition matrix 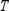 .
. 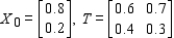
(Multiple Choice)
4.8/5  (24)
(24)
Determine which of the given matrices is an absorbing stochastic matrix.
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)