Multiple Choice
Use the graph to determine the limit visually (if it exists) .Then identify another function g2(x) that agrees with the given function at all but one point.
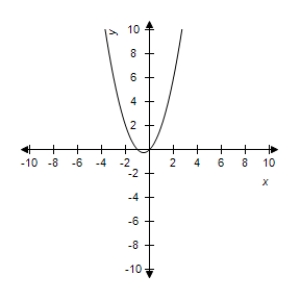
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q242: Find the first five terms of
Q243: Find the limit (if it exists).
Q244: Use the function and its derivative
Q245: Find <span class="ql-formula" data-value="\lim _
Q246: Use the given information to evaluate
Q248: Select correct graph of the following
Q249: Find <span class="ql-formula" data-value="\lim _
Q250: Select the correct graph of the
Q251: Find <span class="ql-formula" data-value="\lim _
Q252: Select the correct graph for the