Multiple Choice
Select the correct graph for the following function using a graphing utility.Determine whether the limit exists or not. ,
A) 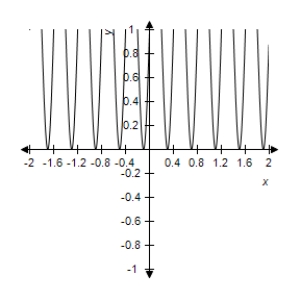
B) 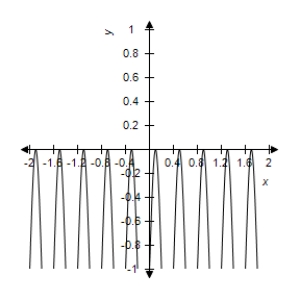
C) 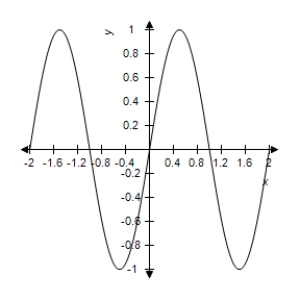
D) 
E)  does not exist
does not exist
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q152: Algebraically evaluate the limit (if it
Q153: Use asymptotes to match <span
Q154: Find the limit of the sequence.
Q155: Use the limit process to find
Q156: Find the limit (if it exists).Round
Q158: Find <span class="ql-formula" data-value="\lim _
Q159: Find <span class="ql-formula" data-value="\lim _
Q160: The average typing speed S (in
Q161: Use the limit process to find
Q162: Rewrite <span class="ql-formula" data-value="\sum _