Multiple Choice
Select from the choices below the slope field for the differential equation.
A) 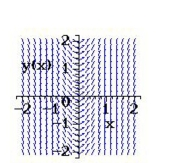
B) 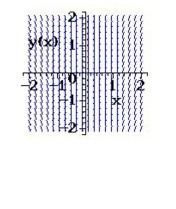
C) 
D) 
E) none of the above
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q43: Use integration to find a general
Q44: A 100-gallon tank is full of
Q45: Select from the choices below the
Q46: A container of hot liquid is
Q47: <span class="ql-formula" data-value="\text { Find the orthogonal
Q49: <span class="ql-formula" data-value="\text { Solve the first-order
Q50: Solve the first order linear differential
Q51: <span class="ql-formula" data-value="\text { The logistic function
Q52: <span class="ql-formula" data-value="\text { The logistic function
Q53: <span class="ql-formula" data-value="\text { Identify the graph