Multiple Choice
Sketch the curve represented by the vector-valued function give the orientation of the curve.
A) 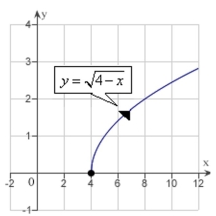
B) 
C) 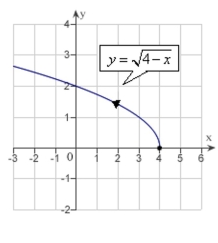
D) 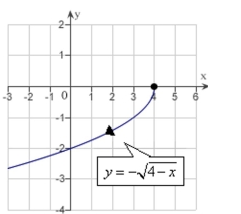
E) 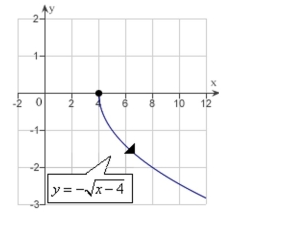
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q55: Find a vector-valued function, using the
Q56: Suppose the outer edge of a
Q57: <span class="ql-formula" data-value="\text { Find } a
Q58: Find the point on the curve
Q59: Find the unit tangent vector <br>
Q61: Find the radius of curvature of
Q62: Find the length of the space
Q63: Find the curvature K of the
Q64: <span class="ql-formula" data-value="\text { Find } \mathbf
Q65: Use the properties of the derivative