A County Real Estate Appraiser Wants to Develop a Statistical

Multiple Choice

A county real estate appraiser wants to develop a statistical model to predict the appraised value of houses in a section of the county called East Meadow. One of the many variables thought to be an important predictor of appraised value is the number of rooms in the house. Consequently, the appraiser decided to fit the simple linear regression model, 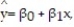where y = appraised value of the house (in $thousands) and x = number of rooms. Using data collected for a sample of n= 74 houses in East Meadow, the following results were obtained: 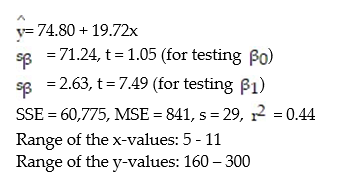Give a practical interpretation of the estimate of the y-intercept of the least squares line.

A) For each additional room in the house, we estimate the appraised value to increase $19,720.
B) For each additional room in the house, we estimate the appraised value to increase $74,800.
C) There is no practical interpretation, since a house with 0 rooms is nonsensical.
D) We estimate the base appraised value for any house to be $74,800.