Solved

Consider the Function F (X) = 5 + 3

Question 2

Multiple Choice

Consider the function f (x) = 5 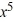Consider the function f (x) = 5 + 3 . Which of the following is the odd periodic extension of f (x) ? A) B) C) D) + 3 Consider the function f (x) = 5 + 3 . Which of the following is the odd periodic extension of f (x) ? A) B) C) D) . Which of the following is the odd periodic extension of f (x) ?


A) Consider the function f (x) = 5 + 3 . Which of the following is the odd periodic extension of f (x) ? A) B) C) D)
B) Consider the function f (x) = 5 + 3 . Which of the following is the odd periodic extension of f (x) ? A) B) C) D)
C) Consider the function f (x) = 5 + 3 . Which of the following is the odd periodic extension of f (x) ? A) B) C) D)
D) Consider the function f (x) = 5 + 3 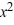. Which of the following is the odd periodic extension of f (x) ? A) B) 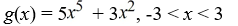C) 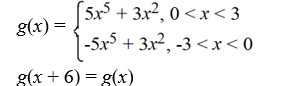D)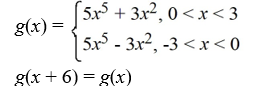

Correct Answer:

verifed

Verified

Related Questions

Q1: The ends of a rod 40 cm

Q3: Consider the following periodic function with period

Q4: Consider the following periodic function with

Q5: Suppose the following initial boundary value problem

Q6: The ends of a rod 45 cm

Q7: Assume that <span class="ql-formula" data-value="\lambda"><span class="katex"><span

Q8: Suppose f (x) is defined by f

Q9: Consider the function f (x) = 7

Q10: Consider the following periodic function with

Q11: Find the Fourier series for f