Solved

Are the Vectors U1 , U2 , and U3 Linearly

Question 34

Essay

Are the vectors u1 , u2 , and u3 linearly independent or linearly dependent? If they are linearly dependent, identify appropriate constants A, B, and C for which A u1 + Bu2 +Cu3 = 0
that demonstrates this fact.
Are the vectors u<sub>1</sub> , u<sub>2</sub> , and u<sub>3</sub> linearly independent or linearly dependent? If they are linearly dependent, identify appropriate constants A, B, and C for which A u<sub>1</sub> + Bu<sub>2</sub> +Cu<sub>3</sub> = 0 that demonstrates this fact.

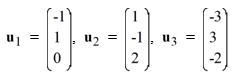
Correct Answer:

verifed

Verified

Linearly dependent.
...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q29: Consider the first-order homogeneous system of linear

Q30: Consider the first-order homogeneous system of linear

Q31: Consider these matrices:<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider these

Q32: Consider the first-order homogeneous system of linear

Q33: Consider the first-order homogeneous system of

Q35: Consider the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="

Q36: Consider the first-order homogeneous system of

Q37: Given that <span class="ql-formula" data-value="\lambda"><span

Q38: Consider the first-order homogeneous system of

Q39: Consider the first-order homogeneous system of