Multiple Choice
Given that = 1 is an eigenvalue of the matrix B = 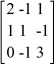 , which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?
, which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?
A) 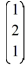 is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.
B)  is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
C)  is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
D)  is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.
Correct Answer:

Verified
Correct Answer:
Verified
Q32: Consider the first-order homogeneous system of linear
Q33: Consider the first-order homogeneous system of
Q34: Are the vectors u<sub>1</sub> , u<sub>2</sub> ,
Q35: Consider the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="
Q36: Consider the first-order homogeneous system of
Q38: Consider the first-order homogeneous system of
Q39: Consider the first-order homogeneous system of
Q40: Are the vectors u<sub>1</sub> , u<sub>2</sub> ,
Q41: Consider the first-order homogeneous system of linear
Q42: Consider the first-order homogeneous system of