Consider the First-Order Homogeneous System of Linear Differential Equations
$\mathbf{x}(t)=C_{1}\left(\begin{array}{c}-1 \\ 0\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{c}-1 \\ 1\end{array}\right)$

Multiple Choice

Consider the first-order homogeneous system of linear differential equations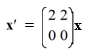

Which of these is the general solution of the system? Here, C₁ and C₂ are arbitrary real constants.

A) $\mathbf{x}(t) =C_{1}\left(\begin{array}{c}-1 \\ 0\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{c}-1 \\ 1\end{array}\right)$
B) $x(t) =C_{1}\left(\begin{array}{c}-1 \\ 0\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{c}1 \\ -1\end{array}\right)$
C) $\mathbf{x}(t) =C_{1}\left(\begin{array}{l}1 \\ 0\end{array}\right) e^{2 t}+C_{2}\left(\begin{array}{c}-1 \\ 1\end{array}\right)$
D) $\mathbf{x}(t) =C_{1}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{2 t}+C_{2}\left(\begin{array}{l}1 \\ -1\end{array}\right)$