Solved

Which of These Are Ordinary Points for the Differential Equation

Question 71

Multiple Choice

Which of these are ordinary points for the differential equation
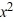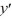(x + 5) Which of these are ordinary points for the differential equation (x + 5) + ( - 49) + 2xy = 0? Select all that apply. A) -5 B) -7 C) 7 D) 0 E) 12 + ( Which of these are ordinary points for the differential equation (x + 5) + ( - 49) + 2xy = 0? Select all that apply. A) -5 B) -7 C) 7 D) 0 E) 12 - 49) Which of these are ordinary points for the differential equation (x + 5) + ( - 49) + 2xy = 0? Select all that apply. A) -5 B) -7 C) 7 D) 0 E) 12 + 2xy = 0?
Select all that apply.


A) -5
B) -7
C) 7
D) 0
E) 12

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q66: Consider the second-order differential equation <img

Q67: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q68: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q69: Consider the first-order differential equation <img

Q70: Consider the first-order differential equation <img

Q72: What is the greatest lower bound for

Q73: x = 0 is a regular singular

Q74: Consider the second-order differential equation <img

Q75: Consider the second-order differential equation <img

Q76: What is a lower bound for the