Consider the First-Order Differential Equation - 10xy = 0 $y(x)=c_{0} e^{\frac{10}{2} x^{2}}$

Multiple Choice

Consider the first-order differential equation - 10xy = 0.
Assume a solution of this equation can be represented as a power series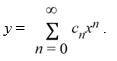
Express the solution y(x) as an elementary function.

A) $y(x) =c_{0} e^{\frac{10}{2} x^{2}}$
B) $y(x) =c_{0} e^{(10 x) ^{2}}$
C) $y(x) =c_{1} e^{10 x}$
D) $y(x) =c_{1} e^{10 x^{2}}$
E) $y(x) =c_{1} e^{(10 x) ^{2}}$