Multiple Choice
Consider the first-order differential equation 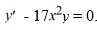
Assume a solution of this equation can be represented as a power series 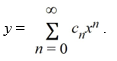 .
.
Assume that C0 is known.
Which of these power series equals y(x) ?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q64: Consider the Bessel equation of order
Q65: Consider the second-order differential equation: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q66: Consider the second-order differential equation <img
Q67: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q68: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q70: Consider the first-order differential equation <img
Q71: Which of these are ordinary points for
Q72: What is the greatest lower bound for
Q73: x = 0 is a regular singular
Q74: Consider the second-order differential equation <img