Solved

Consider the Differential Equation

Question 73

Multiple Choice

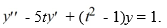
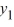Consider the differential equation Consider the differential equation Which of the following statements is true? A) If 2 is a solution of this differential equation, then so is . B) If Y<sub>1</sub> and Y<sub>2</sub> are both solutions of this differential equation, then Y<sub>1</sub> - Y<sub>2</sub> cannot be a solution of it. C) The Principle of Superposition guarantees that if y<sub>1</sub> and y<sub>2</sub> are both solutions of this differential equation, then C<sub>1</sub> y<sub>1</sub> + C<sub>2</sub> y<sub>2</sub> must also be a solution of it, for any choice of real constants and . D) There exist nonzero real constants C<sub>1</sub> and C<sub>2</sub> such that C<sub>1</sub> y<sub>1</sub> - C<sub>2</sub> y<sub>2</sub> is a solution of this differential equation.
Which of the following statements is true?


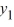A) If 2 Consider the differential equation Which of the following statements is true? A) If 2 is a solution of this differential equation, then so is . B) If Y<sub>1</sub> and Y<sub>2</sub> are both solutions of this differential equation, then Y<sub>1</sub> - Y<sub>2</sub> cannot be a solution of it. C) The Principle of Superposition guarantees that if y<sub>1</sub> and y<sub>2</sub> are both solutions of this differential equation, then C<sub>1</sub> y<sub>1</sub> + C<sub>2</sub> y<sub>2</sub> must also be a solution of it, for any choice of real constants and . D) There exist nonzero real constants C<sub>1</sub> and C<sub>2</sub> such that C<sub>1</sub> y<sub>1</sub> - C<sub>2</sub> y<sub>2</sub> is a solution of this differential equation. is a solution of this differential equation, then so is Consider the differential equation Which of the following statements is true? A) If 2 is a solution of this differential equation, then so is . B) If Y<sub>1</sub> and Y<sub>2</sub> are both solutions of this differential equation, then Y<sub>1</sub> - Y<sub>2</sub> cannot be a solution of it. C) The Principle of Superposition guarantees that if y<sub>1</sub> and y<sub>2</sub> are both solutions of this differential equation, then C<sub>1</sub> y<sub>1</sub> + C<sub>2</sub> y<sub>2</sub> must also be a solution of it, for any choice of real constants and . D) There exist nonzero real constants C<sub>1</sub> and C<sub>2</sub> such that C<sub>1</sub> y<sub>1</sub> - C<sub>2</sub> y<sub>2</sub> is a solution of this differential equation. .
B) If Y1 and Y2 are both solutions of this differential equation, then Y1 - Y2 cannot be a solution of it.
C) The Principle of Superposition guarantees that if y1 and y2 are both solutions of this differential equation, then C1 y1 + C2 y2 must also be a solution of it, for any choice of real constants and .
D) There exist nonzero real constants C1 and C2 such that C1 y1 - C2 y2 is a solution of this differential equation.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q68: Use variation of parameters to find

Q69: Consider this second-order nonhomogeneous differential equation:<br><img

Q70: Which of these is the general

Q71: Suppose a 12-lb object stretches a spring

Q72: Suppose a 10-lb object stretches a spring

Q74: Consider this second-order nonhomogeneous differential equation:<br><img

Q75: Use the method of reduction of order

Q76: Suppose a 160-lb object stretches a spring

Q77: Which of these is the general

Q78: Suppose a 6-lb object stretches a