Suppose a 160-Lb Object Stretches a Spring 3 Feet While

Short Answer

Suppose a 160-lb object stretches a spring 3 feet while in equilibrium, and a dashpot provides a damping force of 3 lbs for every foot per second of velocity. The form of the equation of unforced motion of the object in such a spring-mass system is 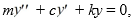where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 1/2 feet below the horizontal with an upward velocity of - 3 feet per second.
After how many seconds does the object pass through the equilibrium position for the first time? Round your answer to the nearest hundredth of a second.