Exam 21: Calculus-Based Optimization
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
The critical point for the function y = 3x2 + 5x + 2 is at
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
Find the critical point for the function y = X3 + 60.This point is a(n)
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
C
The slope of a straight line is constant when measured at any point along the line.
Free
(True/False)
4.8/5  (45)
(45)
Correct Answer:
True
The first step in attempting to find a minimum or maximum of a nonlinear function is to take the derivative of the function, set it equal to zero, and solve for x.
(True/False)
5.0/5  (44)
(44)
The second derivative of the function 4 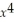 + 3
+ 3 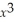 + 2
+ 2 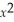 + x + 7 is 48
+ x + 7 is 48 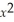 + 18x.
+ 18x.
(True/False)
4.9/5  (38)
(38)
At a minimum of a nonlinear function, the first derivative is equal to zero, and the second derivative is positive.
(True/False)
4.9/5  (37)
(37)
If, for a nonlinear function, the first derivative is equal to zero and the second derivative is equal to zero, we have both a maximum and a minimum occurring simultaneously.
(True/False)
4.8/5  (32)
(32)
The points of inflection of the curve 
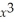 +
+ 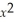 + x + 12 are X = 1 and X = -1.
+ x + 12 are X = 1 and X = -1.
(True/False)
4.9/5  (27)
(27)
The EOQ model is obtained by taking the second derivative of the revenue function.
(True/False)
4.8/5  (35)
(35)
Find the point at which the following function has an inflection point: y = 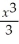 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
(Multiple Choice)
4.8/5  (32)
(32)
We can find a point of inflection by simply setting the second derivative of the nonlinear function equal to zero and solving.
(True/False)
4.9/5  (36)
(36)
Find the slope of the line Y = 4X-3 at the point where X = 17.
(Short Answer)
4.9/5  (44)
(44)
Through rigorous quantitative analysis, Geoff develops a trading algorithm that will permit him to gain a competitive advantage over his previous dartboard method of selecting stocks.What he has noticed is that a stock's value at the end of the month can be accurately forecast using the equation PriceEND = 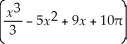 + PriceSTART where PriceSTART is the stock price at the start of the month and x is the number of days until the next full moon.At what point in time will the stock be at its maximum and minimum? If SBUX is trading at $50 per share at the start of the month, what profit can Geoff realize if he buys 100 shares at its minimum price and sells all 100 shares at its maximum price.Assume Geoff pays a $10 fee for the buy order and another $10 for the sell order.
+ PriceSTART where PriceSTART is the stock price at the start of the month and x is the number of days until the next full moon.At what point in time will the stock be at its maximum and minimum? If SBUX is trading at $50 per share at the start of the month, what profit can Geoff realize if he buys 100 shares at its minimum price and sells all 100 shares at its maximum price.Assume Geoff pays a $10 fee for the buy order and another $10 for the sell order.
(Essay)
4.8/5  (30)
(30)
To maximize total revenues, one can set the derivative of the total revenue function equal to zero and solve.
(True/False)
4.8/5  (39)
(39)
Showing 1 - 20 of 39
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)