Exam 17: Dynamic Programming
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
Alex takes a troop of boy scouts on a hike one weekend.A corpulent young entrepreneur decides to carry a few extra items to sell to his captive audience.His backpack has room for 13 pounds of provisions beyond the necessary pocketknife and tent.The weights of the most popular snacks are as follows: 12 ounces for item A, 3 ounces for item B, 6 ounces for item C and 16 ounces for item D.His net profit for these items are $1.50 for A, $0.50 for B, $1.00 for C, and $2.50 for D.He scans the pantry at his house before packing his backpack and notes that he has available 24 A's, 16 B's, 12 C's, and 10 D's.Use dynamic programming to determine the maximum possible profits that may be generated.
Free
(Short Answer)
4.9/5  (34)
(34)
Correct Answer:
Maximum profit $33.50.Carry 13 B's, 12 C's and 6 D's.
Dynamic programming can only be used to solve network-based problems.
Free
(True/False)
4.9/5  (28)
(28)
Correct Answer:
False
Discuss, briefly, the role of the transformation function.
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
The transformation function defines the relationship between stages in the dynamic programming problem.
Discuss, briefly, the difference between a decision variable and a state variable.
(Essay)
4.9/5  (39)
(39)
The data below is a dynamic programming solution for a shortest route problem.
 -According to Table M2-2, which gives a solution to a shortest route problem solved with dynamic programming, the total distance from City 1 to City 7 is 14.What is the shortest distance from City 3 to City 7?
-According to Table M2-2, which gives a solution to a shortest route problem solved with dynamic programming, the total distance from City 1 to City 7 is 14.What is the shortest distance from City 3 to City 7?
(Multiple Choice)
4.8/5  (33)
(33)
There are four items (A, B, C, and D) that are to be shipped by truck. The weights of these are 3, 7, 4, and 5 tons, respectively, and the plane can carry 13 tons. The profits (in thousands of dollars) generated by these are 3 for A, 4 for B, 2 for C, and 5 for D. There are three units of each available for shipment. The maximum possible profit for this would be
(Multiple Choice)
4.8/5  (39)
(39)
The data below details the distances that a delivery service must travel.Use dynamic programming to solve for the shortest route from City 1 to City 8.
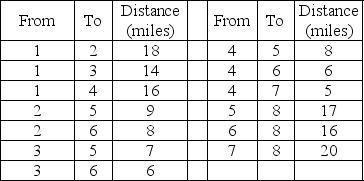
(Short Answer)
4.7/5  (41)
(41)
There are three items (A, B, and C) that are to be shipped by air. The weights of these are 4, 5, and 3 tons, respectively. The profits (in thousands of dollars) generated by these are 6 for A, 7 for B, and 5 for C. A total of 14 tons may be carried by the plane. There are four units of each available for shipment. What is the maximum possible profit for this situation?
(Multiple Choice)
4.8/5  (31)
(31)
Develop the shortest-route network for the problem below, and determine the minimum distance from node 1 to node 7.
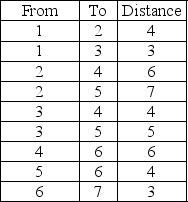
(Short Answer)
4.9/5  (43)
(43)
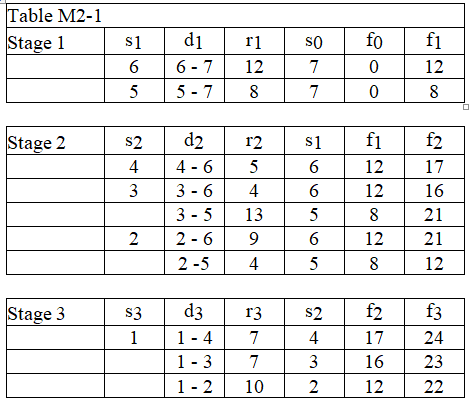
The data below is a dynamic programming solution for a shortest route problem.
 -Using the data in Table M2-1, determine the optimal arc of stage 2.
-Using the data in Table M2-1, determine the optimal arc of stage 2.
(Multiple Choice)
5.0/5  (34)
(34)
The data below is a dynamic programming solution for a shortest route problem.
 -According to Table M2-2, which gives a solution to a shortest route problem solved with dynamic programming, which cities would be included in the best route?
-According to Table M2-2, which gives a solution to a shortest route problem solved with dynamic programming, which cities would be included in the best route?
(Multiple Choice)
4.7/5  (39)
(39)
For knapsack problems, sn-1 = an × sn + bn × dn + cn is a typical transformation expression.
(True/False)
4.8/5  (35)
(35)
There are four items (A, B, C, and D)that are to be shipped by air.The weights of these are 5, 7, 8, and 11 tons, respectively.The profits (in thousands of dollars)generated by these are 5 for A, 8 for B, 7 for C, and 10 for D.There are 3 units of A, 4 unit of B, 6 units of C, and 5 units of D available to be shipped.The maximum weight is 44 tons.Use dynamic programming to determine the maximum possible profits that may be generated.
(Short Answer)
4.9/5  (25)
(25)
There are six cities (City 1-City 6) serviced by a particular airline. Limited routes are available, and the distances for each of these routes are presented in the table below.
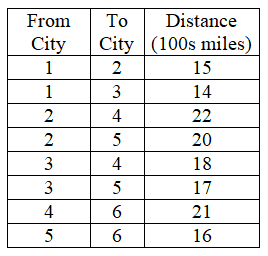 -What is the shortest route between City 1 and City 5?
-What is the shortest route between City 1 and City 5?
(Multiple Choice)
4.8/5  (38)
(38)
The following information describes a shortest-route problem with the distance in miles.How many stages will this dynamic problem have? 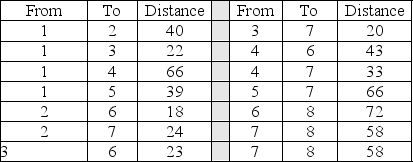
(Multiple Choice)
4.8/5  (37)
(37)
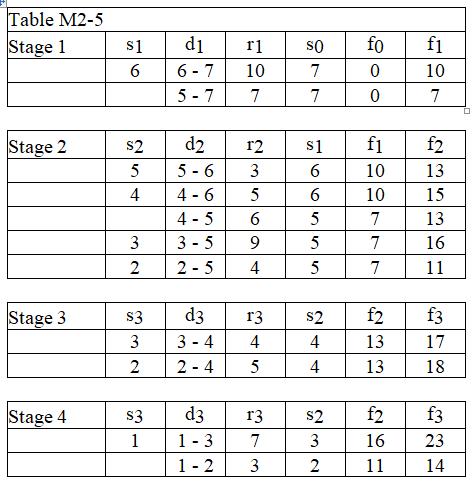 -Using the data in Table M2-5, determine the optimal distance of stage 1.
-Using the data in Table M2-5, determine the optimal distance of stage 1.
(Multiple Choice)
4.8/5  (30)
(30)
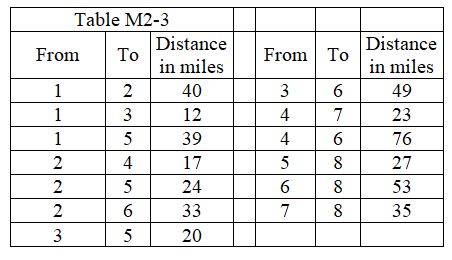 -For the shortest route problem described in Table M2-3, what is the distance for the shortest route?
-For the shortest route problem described in Table M2-3, what is the distance for the shortest route?
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)