Exam 8: Linear Programming Applications
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
A manufacturer of microcomputers produces four models: Portable, Student, Office, and Network.The profit per unit on each of these four models is $500, $350, $700, and $1000, respectively.The models require the labor and materials per unit shown below.
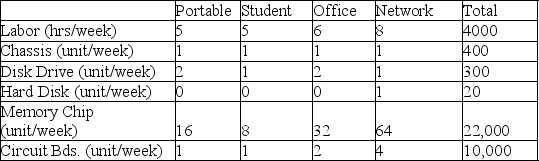 How many of each model should be produced to maximize profit.What is the maximum profit?
How many of each model should be produced to maximize profit.What is the maximum profit?
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
Let X1 = portable
X2 = student
X3 = office
X4 = network
Maximize 500X1 + 350X2 + 700X3 + 1000X4
Subject to: 5X1 + 5X2 + 6X3 + 8X4 ≤ 4000
X1 + X2 + X3 + X4 ≤ 400
2X1 + X2 + 2X3 + X4 ≤ 300
X4 ≤ 20
16X1 + 8X2 + 32X3 + 64X4 ≤ 22,000
X1 + X2 + 2X3 + 4X4 ≤ 10,000
X1, X2, X3, X4 ≥ 0
X1 = 0, X2 = 56, X3 = 112, X4 = 20; Maximum profit = $118,000
The selection of specific investments from among a wide variety of alternatives is the type of LP problem known as
Free
(Multiple Choice)
4.9/5  (44)
(44)
Correct Answer:
D
Ivana Miracle wishes to invest up to her full inheritance of $300,000, and her goal is to minimize her risk subject to an expected annual return of at least $30,000.She has decided to invest her money in any of three possible ways-CDs, which pay a guaranteed 6 percent; stocks, which have an expected return of 15 percent; and a money market mutual fund, which is expected to return 8 percent.Risk factors are 1.0 for the CDs, 3.6 for the stocks, and 1.8 for the money market fund.Formulate this as a linear program.
Free
(Essay)
4.7/5  (36)
(36)
Correct Answer:
Let C = dollars invested in CDs
Let S = dollars invested in stocks
Let M = dollars invested in the money market mutual fund
Minimize C + 3.6S + 1.8M
Subject to: 0.06C + 0.15S + 0.08M ≥ 30,000
C + S + M ≤ 300,000
C,S,M ≥ 0
Blending problems arise when one must decide which of two or more ingredients is to be chosen to produce a product.
(True/False)
4.8/5  (41)
(41)
A mail order firm, AmazingCo, can use one of 3 shipping couriers.Ajax Shipping charges $6 per pound and delivers in 2 days.Bilco Lanes charges $9 per pound but guarantees next day delivery.The final courier, Hobo Ltd., charges only $3 per pound but takes 4 days to deliver.AmazingCo has a quarterly budget of $280,000 and a reputation for timely delivery.Formulate the linear program so that the firm delivers as fast as possible within budget for 70,000 pounds of shipments per quarter.
Let X1 = pounds using Ajax
X2 = pounds using Bilco
X3 = pounds using Hobo
(Essay)
4.7/5  (41)
(41)
Table 8-9
As the high bidder on a monstrous storage locker in Rancho Cucamonga, Darrell discovers much to his dismay that no collectibles or priceless works of art have been seeded in his locker. Instead he finds cases and cases of raw leather, zippers, packets of dye, and spools of thread. After some thorough research on typical prices, Darrell concludes that his cost of the leather is $2 per yard, his zipper cost if $1 per foot, the dye is $1 per packet and the thread is fifty cents per foot.
They don't call him "The Gambler" for nothing, and he is determined to find a way to profit from this misfortune as well as shed the burden of his son Brandon, who isn't much of an asset in the storage wars. He sets Brandon up with a small production business and, using his connections, manages to land contracts to supply leather purses, pants, backpacks and jackets that can be dyed to match current market trends. "In fashion, one day you're in and the next day you're out," Darrell explains to Brandon as he reviewed the contracts he had arranged. "We can make enough to get you out of the house now that I have 60,000 yards of leather, 50,000 feet of zipper material, 100,000 dye packets and 200,000 feet of thread."
One local distributer has placed an order for at least 5,000 purses and is willing to increase the order to a maximum of 10,000 if sales are strong. A purse requires 0.25 yards of leather, a one foot length of zipper material, one dye packet and two feet of thread. Darrell charges $41.50 for each one shipped. Another distributor is more interested in apparel and has placed orders for both pants at $33.50 and jackets at $104. They want at least 10,000 jackets up to a ceiling of 15,000 and at least 10,000 pairs of leather pants. As you might imagine, there is no limit to the number of pairs of leather pants that can be sold. A leather jacket requires 1.5 yards of leather, three feet of zipper material, two dye packets and eight feet of thread. Leather pants take a full two yards of leather, six inches of zipper material, two dye packets and six feet of thread. Yet another distributor is keen on backpacks and sees a market for at least 2,500 backpacks but is unwilling to take more than 7,500. Each backpack requires a half yard of leather, two feet of zipper material, one dye packet, and three feet of thread, and Darrell ships them to this distributor at $22.50.
-Use the information in Table 8-9 to formulate an LP approach to profit maximization.How many constraints (exclusive of the non-negativity constraint)should this problem have?
(Multiple Choice)
4.9/5  (31)
(31)
When formulating transportation LP problems, the objective function usually deals with the
(Multiple Choice)
4.8/5  (32)
(32)
Three types of gasoline are manufactured by a company - Regular, Super, and Extra.Regular should have at least 11 percent additive 1 and 17 percent additive 2.Super should have at least 13 percent additive 1 and 22 percent additive 2.Extra should have at least 17 percent additive 1 and 19 percent additive 2.These are made by using two crudes - A and B.Crude A cost $28 per barrel and is 14 percent additive 1 and 18 percent additive 2.Crude B costs $30 per barrel and is 20 percent additive 1 and 24 percent additive 2.The demand for Regular is projected to be 1,000 barrels, while each of the others has a demand of 2,000 barrels.Formulate this as a linear programming problem to minimize cost while meeting all constraints.Carefully define all decision variables.
(Essay)
4.8/5  (35)
(35)
Determining the mixture of ingredients for a most economical feed or diet combination would be described as a production mix type of linear program.
(True/False)
4.9/5  (38)
(38)
A manufacturer of microcomputers produces four models: Portable, Student, Office, and Network.The profit per unit on each of these four models is $500, $350, $700, and $1000, respectively.The models require the labor and materials per unit shown below.
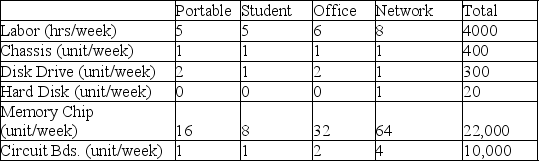 Formulate this product mix problem using linear programming.
Formulate this product mix problem using linear programming.
(Essay)
4.7/5  (31)
(31)
An ingredient or blending problem is a special case of the more general problem known as diet and feed mix problems.
(True/False)
5.0/5  (42)
(42)
A typical constraint in the portfolio selection problem formulated in LP would be to maintain risk below some specified amount.
(True/False)
4.8/5  (35)
(35)
A computer start-up named Pear is considering entering the U.S.market with what they believe to be a smaller and faster computer than some of the existing products on the market.They want to get a feel for whether or not customers would be willing to switch from some of the existing bigger brands to consider their product.They want to collect a reasonable sample from across the United States representative of all age brackets.They have split the United States into 2 regions: East and West.They want at least 65% of their sample to cover the East and no fewer than 25% of the West.They also have divided the age groups into 3 categories: 18-35, 36-69, and 70 and up.They want at least 50% of their sample to be between 18 and 35 and at least 40% to be between 36 and 69.The costs per person surveyed is given in the table below:
 Assume that at least 1,000 people are to be surveyed.The problem is for Pear Company to decide how many people to survey from each age bracket within each region in order to minimize costs while meeting requirements.Formulate this problem as a linear program.
Assume that at least 1,000 people are to be surveyed.The problem is for Pear Company to decide how many people to survey from each age bracket within each region in order to minimize costs while meeting requirements.Formulate this problem as a linear program.
(Essay)
4.7/5  (37)
(37)
Dr.Barry Soprano wishes to invest his retirement fund of $2,200,000 so that his return on investment is maximized, but he also wishes to keep the risk level relatively low.He has decided to invest his money in any of three possible ways: CDs that pay a guaranteed 5 percent; stocks that have an expected return of 22 percent; and a loan sharking business that is expected to return 58 percent.He has decided that the total $2,200,000 will be invested, but any part (or all)of it may be put in any of the three alternatives.Thus, he may have some money invested in all three alternatives.He has also decided to invest, at most, 50 percent of this in loansharking and at least 20 percent of this in CDs.Formulate this as a linear programming problem and solve in Excel.
(Essay)
4.7/5  (28)
(28)
Three types of fertilizer are manufactured by a company: Regular, Supergro, and Jungle Feeder.Regular should have at least 10 percent nitrogen and 16 percent phosphorous.Supergro should have at least 12 percent nitrogen and 20 percent phosphorous, and Jungle Feeder should have at least 15 percent nitrogen and 18 percent phosphorous.These are made by using two components: A and B.Component A costs $0.30 per pound and is 14 percent nitrogen and 18 percent phosphorous.Component B costs $0.50 per pound and is 20 percent nitrogen and 24 percent phosphorous.The demand for Regular is projected to be 1,000 pounds, while each of the others has a demand of 2,000 pounds.Formulate the appropriate linear program.
Let X1 = pounds of component A in Regular
X2 = pounds of component A in Supergro
X3 = pounds of component A in Jungle Feeder
X4 = pounds of component B in Regular
X5 = pounds of component B in Supergro
X6 = pounds of component B in Jungle Feeder
(Essay)
4.8/5  (37)
(37)
Table 8-9
As the high bidder on a monstrous storage locker in Rancho Cucamonga, Darrell discovers much to his dismay that no collectibles or priceless works of art have been seeded in his locker. Instead he finds cases and cases of raw leather, zippers, packets of dye, and spools of thread. After some thorough research on typical prices, Darrell concludes that his cost of the leather is $2 per yard, his zipper cost if $1 per foot, the dye is $1 per packet and the thread is fifty cents per foot.
They don't call him "The Gambler" for nothing, and he is determined to find a way to profit from this misfortune as well as shed the burden of his son Brandon, who isn't much of an asset in the storage wars. He sets Brandon up with a small production business and, using his connections, manages to land contracts to supply leather purses, pants, backpacks and jackets that can be dyed to match current market trends. "In fashion, one day you're in and the next day you're out," Darrell explains to Brandon as he reviewed the contracts he had arranged. "We can make enough to get you out of the house now that I have 60,000 yards of leather, 50,000 feet of zipper material, 100,000 dye packets and 200,000 feet of thread."
One local distributer has placed an order for at least 5,000 purses and is willing to increase the order to a maximum of 10,000 if sales are strong. A purse requires 0.25 yards of leather, a one foot length of zipper material, one dye packet and two feet of thread. Darrell charges $41.50 for each one shipped. Another distributor is more interested in apparel and has placed orders for both pants at $33.50 and jackets at $104. They want at least 10,000 jackets up to a ceiling of 15,000 and at least 10,000 pairs of leather pants. As you might imagine, there is no limit to the number of pairs of leather pants that can be sold. A leather jacket requires 1.5 yards of leather, three feet of zipper material, two dye packets and eight feet of thread. Leather pants take a full two yards of leather, six inches of zipper material, two dye packets and six feet of thread. Yet another distributor is keen on backpacks and sees a market for at least 2,500 backpacks but is unwilling to take more than 7,500. Each backpack requires a half yard of leather, two feet of zipper material, one dye packet, and three feet of thread, and Darrell ships them to this distributor at $22.50.
-Use the information in Table 8-9 to formulate a constraint for the use of zipper material.
(Multiple Choice)
4.9/5  (29)
(29)
Cedar Point amusement park management is preparing the park's annual promotional plan for the coming season.Several advertising alternatives exist: newspaper, television, radio, and displays at recreational shows.The information below shows the characteristics associated with each of the advertising alternatives, as well as the maximum number of placements available in each medium.Given an advertising budget of $250,000, how many placements should be made in each medium to maximize total audience exposure? Formulate this as a linear programming problem.
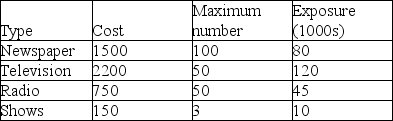
(Essay)
4.7/5  (35)
(35)
When formulating transportation LP problems, constraints usually deal with the
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 89
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)