Exam 7: Linear Programming Models: Graphical and Computer Methods
Exam 1: Introduction to Quantitative Analysis71 Questions
Exam 2: Probability Concepts and Applications157 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models133 Questions
Exam 5: Forecasting111 Questions
Exam 6: Inventory Control Models123 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods110 Questions
Exam 8: Linear Programming Applications105 Questions
Exam 9: Transportation,assignment,and Network Models98 Questions
Exam 10: Integer Programming,goal Programming,and Nonlinear Programming98 Questions
Exam 11: Project Management134 Questions
Exam 12: Waiting Lines and Queuing Theory Models145 Questions
Exam 13: Simulation Modeling79 Questions
Exam 14: Markov Analysis86 Questions
Exam 15: Statistical Quality Control98 Questions
Exam 16: Analytic Hierarchy Process53 Questions
Exam 17: Dynamic Programming67 Questions
Exam 18: Decision Theory and the Normal Distribution50 Questions
Exam 19: Game Theory47 Questions
Exam 20: Mathematical Tools: Determinants and Matrices99 Questions
Exam 21: Calculus-Based Optimization24 Questions
Exam 22: Linear Programming: The Simplex Method100 Questions
Exam 23: Transportation, Assignment, and Network Algorithms111 Questions
Select questions type
Consider the sensitivity report below: 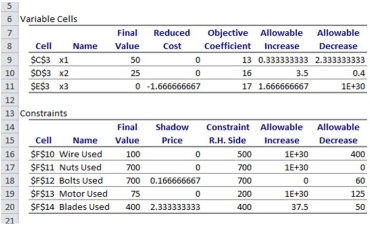 (a)Which constraints are binding?
(b)Which constraints are non-binding?
(c)What is the increase in the objective value if 10 blades are added?
(a)Which constraints are binding?
(b)Which constraints are non-binding?
(c)What is the increase in the objective value if 10 blades are added?
(Essay)
4.8/5  (37)
(37)
When a constraint line bounding a feasible region has the same slope as an isoprofit line,
(Multiple Choice)
5.0/5  (44)
(44)
A plastic parts supplier produces two types of plastic parts used for electronics.Type 1 requires 30 minutes of labor and 45 minutes of machine time.Type 2 requires 60 minutes of machine hours and 75 minutes of labor.There are 600 hours available per week of labor and 800 machine hours available.The demand for custom molds and plastic parts are identical.Type 1 has a profit margin of $25 a unit and Type 2 has a profit margin of $45 a unit.The plastic parts supplier must choose the quantity of Product A and Product B to produce which maximizes profit.
(a)Formulate this as a linear programming problem.
(b)Find the solution that gives the maximum profit using either QM for Windows or Excel.
(Essay)
4.8/5  (39)
(39)
Which of the following is not acceptable as a constraint in a linear programming problem (maximization)? 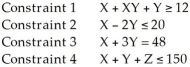
(Multiple Choice)
4.8/5  (45)
(45)
A straight line representing all non-negative combinations of X1 and X2 for a particular profit level is called a(n)
(Multiple Choice)
4.8/5  (29)
(29)
Susanna Nanna is the production manager for a furniture manufacturing company.The company produces tables (X)and chairs (Y).Each table generates a profit of $80 and requires 3 hours of assembly time and 4 hours of finishing time.Each chair generates $50 of profit and requires 3 hours of assembly time and 2 hours of finishing time.There are 360 hours of assembly time and 240 hours of finishing time available each month.The following linear programming problem represents this situation.
Maximize 80X + 50Y
Subject to: 3X + 3Y ≤ 360
4X + 2Y ≤ 240
X,Y ≥ 0
The optimal solution is X = 0,and Y = 120.
(a)What would the maximum possible profit be?
(b)How many hours of assembly time would be used to maximize profit?
(c)If a new constraint,2X + 2Y ≤ 400,were added,what would happen to the maximum possible profit?
(Essay)
4.9/5  (45)
(45)
Consider the following constraints from a linear programming problem: 2X + Y ≤ 200
X + 2Y ≤ 200
X,Y ≥ 0
If these are the only constraints,which of the following points (X,Y)cannot be the optimal solution?
(Multiple Choice)
4.9/5  (25)
(25)
Consider the following linear programming problem: 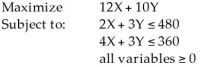 The maximum possible value for the objective function is
The maximum possible value for the objective function is
(Multiple Choice)
4.7/5  (42)
(42)
As a supervisor of a production department,you must decide the daily production totals of a certain product that has two models,the Deluxe and the Special.The profit on the Deluxe model is $12 per unit and the Special's profit is $10.Each model goes through two phases in the production process,and there are only 100 hours available daily at the construction stage and only 80 hours available at the finishing and inspection stage.Each Deluxe model requires 20 minutes of construction time and 10 minutes of finishing and inspection time.Each Special model requires 15 minutes of construction time and 15 minutes of finishing and inspection time.The company has also decided that the Special model must comprise at least 40 percent of the production total.
(a)Formulate this as a linear programming problem.
(b)Find the solution that gives the maximum profit.
(Essay)
4.9/5  (34)
(34)
The mathematical theory behind linear programming states that an optimal solution to any problem will lie at a(n)________ of the feasible region.
(Multiple Choice)
4.8/5  (38)
(38)
If the addition of a constraint to a linear programming problem does not change the solution,the constraint is said to be
(Multiple Choice)
4.8/5  (33)
(33)
Which of the following is not a property of all linear programming problems?
(Multiple Choice)
4.8/5  (27)
(27)
Determine where the following two constraints intersect.
2X - 4Y = 800
−X + 6Y ≥ -200
(Essay)
4.8/5  (33)
(33)
Showing 41 - 60 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)