Exam 3: The Nature of Logic
Exam 1: The Nature of Problem Solving53 Questions
Exam 2: The Nature of Sets64 Questions
Exam 3: The Nature of Logic160 Questions
Exam 4: The Nature of Numeration Systems102 Questions
Exam 5: The Nature of Numbers139 Questions
Exam 6: The Nature of Algebra173 Questions
Exam 7: The Nature of Geometry139 Questions
Exam 8: The Nature of Measurement50 Questions
Exam 9: The Nature of Networks and Graph Theory76 Questions
Exam 10: The Nature of Growth57 Questions
Exam 11: The Nature of Sequences, Series, and Financial Management130 Questions
Exam 12: The Nature of Counting78 Questions
Exam 13: The Nature of Probability97 Questions
Exam 14: The Nature of Statistics82 Questions
Exam 15: The Nature of Graphs and Functions74 Questions
Exam 16: The Nature of Mathematical Systems97 Questions
Exam 17: The Nature of Voting and Apportionment52 Questions
Select questions type
Write the symbolic statement that follows from the given statement. To qualify for a loan, the applicant must have a gross income of at least $40,000 if single or combined income of $54,000 if married. Let
Q: You qualify for a loan.
M:You are married.
I: You have an income of at least $40,000.
B: You spouse has an income of at least $40,000.
(Multiple Choice)
4.9/5  (39)
(39)
Translate the sentence into if-then form. All work is noble.
If it is __________, then it __________.
(Multiple Choice)
4.8/5  (44)
(44)
Using AND-gates, OR-gates, and NOT-gates, design a circuit that would find the truth values for the sentence. 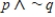
Select the correct circuit.
Select the correct circuit.
(Multiple Choice)
4.9/5  (39)
(39)
Translate the following statement into symbols.
Marsha finished the sign, or the table and a pair of chairs.
Use s for sign, t for table, and c for chairs.
(Multiple Choice)
4.7/5  (34)
(34)
Form a valid conclusion, using all the statements for each argument. Give reasons.
If you learn mathematics, then you are intelligent.
If you are intelligent, then you understand politics.
(Multiple Choice)
4.7/5  (42)
(42)
Determine whether the argument in the problem below is valid or invalid. If valid, name the type of reasoning and if invalid, determine the error in reasoning. Assume that if a number is odd, then it is not even.
If a3 is even, then a must be even.
A is odd.
Therefore, a3 is odd.
(Multiple Choice)
4.8/5  (29)
(29)
Determine whether the argument is valid or invalid. If valid, name the type of reasoning and if invalid, determine the error in reasoning. No students are enthusiastic.
You are enthusiastic.
Therefore, you are not a student.
(Multiple Choice)
4.9/5  (41)
(41)
Write the converse of the given statement.
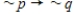
Please use => for the sign
Please use => for the sign 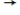 .
.
(Short Answer)
4.8/5  (24)
(24)
Form a valid conclusion, using all the statements for each argument. Give reasons.
If you learn economics, then you are intelligent.
If you are intelligent, then you understand human nature.
If you __________(learn, don't learn) economics, then you __________ (understand, don't understand) human nature.
__________ (direct, indirect, transitive)
(Short Answer)
4.9/5  (40)
(40)
Determine the truth value of the given statement.
Let 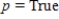 and
and 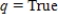 .
either p or q
.
either p or q
(True/False)
4.8/5  (39)
(39)
Determine whether the argument in the problem below is valid or invalid. If valid, name the type of reasoning and if invalid, determine the error in reasoning.
If 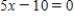 , then
, then 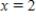 .
. 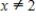 Therefore,
Therefore, 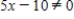 .
.
(Multiple Choice)
4.8/5  (46)
(46)
Showing 141 - 160 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)