Exam 17: The Nature of Voting and Apportionment
Exam 1: The Nature of Problem Solving53 Questions
Exam 2: The Nature of Sets64 Questions
Exam 3: The Nature of Logic160 Questions
Exam 4: The Nature of Numeration Systems102 Questions
Exam 5: The Nature of Numbers139 Questions
Exam 6: The Nature of Algebra173 Questions
Exam 7: The Nature of Geometry139 Questions
Exam 8: The Nature of Measurement50 Questions
Exam 9: The Nature of Networks and Graph Theory76 Questions
Exam 10: The Nature of Growth57 Questions
Exam 11: The Nature of Sequences, Series, and Financial Management130 Questions
Exam 12: The Nature of Counting78 Questions
Exam 13: The Nature of Probability97 Questions
Exam 14: The Nature of Statistics82 Questions
Exam 15: The Nature of Graphs and Functions74 Questions
Exam 16: The Nature of Mathematical Systems97 Questions
Exam 17: The Nature of Voting and Apportionment52 Questions
Select questions type
An elderly rancher died and left her estate to her three children. She bequeathed her 71 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 71 belonging to the estate, and then told each child to pick from among the 72 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took thirty six horses, the second child took twenty four, and the third child, eight. The 71 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 36 horses (but was entitled to only 71/2 = 35.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
(Multiple Choice)
4.8/5  (34)
(34)
In voting among three candidates, the outcomes are reported as: 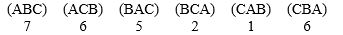 How many voters did rank three candidates in the order of C first, A next, and candidate B last?
How many voters did rank three candidates in the order of C first, A next, and candidate B last?
(Multiple Choice)
4.9/5  (38)
(38)
Consider the following situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes):  Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
(Multiple Choice)
4.9/5  (30)
(30)
An elderly rancher died and left her estate to her three children. She bequeathed her 17 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. They informed the judge that the 17 horses were not of equal value. The children agreed on a ranking of the 17 horses (#1 being the best and #17 being a real dog of a horse). They asked the judge to divide the estate fairly so that each child would receive not only the correct number of horses but horses whose average rank would also be the same. For example, if a child received horses 1 and 17, the number of horses is two and the average value is 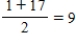 . How did the judge apportion the horses?
. How did the judge apportion the horses?
(Essay)
4.8/5  (29)
(29)
The Adobe School District is hiring a vice principal and has interviewed four candidates: Anna (A), Bono (B), Clark (C), and David (D). The hiring committee has indicated their preferences. 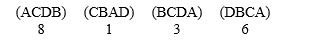 Who is the winner using the plurality method? Answer A, B, C, or D.
Do the results of the previous questions violate the irrelevant alternatives criterion? Answer yes or no.
Suppose that Bono drops out of the running before the vote is taken. Who is the winner using the plurality method? Answer A, B, C, or D.
Who is the winner using the plurality method? Answer A, B, C, or D.
Do the results of the previous questions violate the irrelevant alternatives criterion? Answer yes or no.
Suppose that Bono drops out of the running before the vote is taken. Who is the winner using the plurality method? Answer A, B, C, or D.
(Short Answer)
4.8/5  (44)
(44)
The seniors at a high school are voting for where to go for their senior trip. They are deciding on Apple Valley (A), Bend Canyon (B), Crystal River (C), or Danger Gap (D). The results of the preferences are: 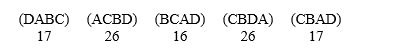 Who wins using the pairwise comparison method? Answer A, B, C, or D.
Does this violate the Condorcet criterion? Answer yes or no.
Who wins using the pairwise comparison method? Answer A, B, C, or D.
Does this violate the Condorcet criterion? Answer yes or no.
(Short Answer)
4.8/5  (28)
(28)
Suppose your college transcripts show the distribution of grades: 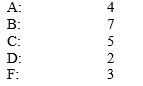 Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
(Multiple Choice)
5.0/5  (31)
(31)
In voting among four candidates, the outcomes are reported as: 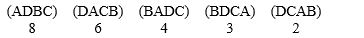 How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
(Multiple Choice)
4.8/5  (34)
(34)
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 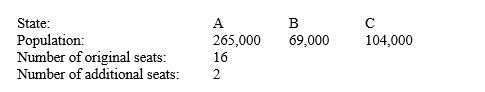
(Multiple Choice)
4.8/5  (43)
(43)
An elderly rancher died and left her estate to her three children. She bequeathed her 35 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 35 belonging to the estate, and then told each child to pick from among the 36 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took eighteen horses, the second child took twelve, and the third child, four. The 35 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 18 horses (but was entitled to only 35/2 = 17.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
__________ (Adams' plan and Jefferson's plan, Webster's plan and Jefferson's plan, Adams' plan and Webster's plan, Adams' plan, None of the plans)
(Short Answer)
4.9/5  (39)
(39)
Suppose your college transcripts show the distribution of grades: 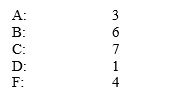
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
Which voting method describes how you answered previous question? Answer majority method, plurality method, borda count method, hare method, pairwise comparison method, tournament method, or approval method.
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
Which voting method describes how you answered previous question? Answer majority method, plurality method, borda count method, hare method, pairwise comparison method, tournament method, or approval method.
(Short Answer)
4.7/5  (28)
(28)
A focus group of 32 people for ABC TV were asked to rank the government spending priorities of education (E), military spending (M), health care (H), immigration (I), and lowering taxes (T). Here are the preferences:
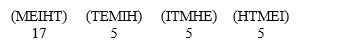
Suppose that the losing issues of immigration, health care, and health care are removed from the table. Now, who is the winner using the Borda count method? AnswerE, H, M, I, or T.
Does the Borda count method violate the irrelevant alternatives criterion? Answer yes or no.
Suppose that the losing issues of immigration, health care, and health care are removed from the table. Now, who is the winner using the Borda count method? AnswerE, H, M, I, or T.
Does the Borda count method violate the irrelevant alternatives criterion? Answer yes or no.
(Short Answer)
4.8/5  (32)
(32)
If there are 10 voters and 5 candidates, how many total points would there be in a Borda count?
__________ points
(Short Answer)
4.8/5  (30)
(30)
Consider the situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes):  How many possible rankings are there?
How many possible rankings are there?
(Multiple Choice)
4.9/5  (33)
(33)
Use Jefferson's plan. Which state does violate the quota rule? 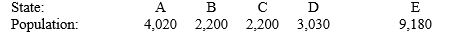 Number of seats:
Number of seats:  200
200
(Multiple Choice)
4.9/5  (28)
(28)
A fair apportionment of dividing a leftover piece of cake between two children is to let child #1 cut the cake into two pieces and then to let child #2 pick which piece he or she wants. Consider the following apportionment of dividing the leftover piece of cake among three children. Let the first child cut the cake into two pieces. Then the second child is permitted to cut one of those pieces into two parts. Child #3 can select any of the pieces, followed by child #1 selecting one of the remaining pieces, followed by child #2 who gets the remaining piece. Is this allocation process fair if each child's goal is to maximize the size of his or her own piece of cake?
(Multiple Choice)
4.8/5  (32)
(32)
Consider the situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes): 
How many possible rankings are there?
How many possible rankings are there?
(Short Answer)
4.8/5  (31)
(31)
The fraternity is electing a national president and there are four candidates: Alberto (A), Bate (B), Carl (C), and Dave (D). The voter preferences are: 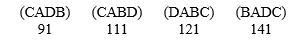 Who wins the election using the Hare method? Does this violate any of the fairness criteria?
Who wins the election using the Hare method? Does this violate any of the fairness criteria?
(Multiple Choice)
4.8/5  (33)
(33)
In voting among three candidates, the outcomes are reported as: 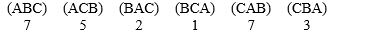 Determine the winner, if any, using Hare method.
Determine the winner, if any, using Hare method.
(Multiple Choice)
4.8/5  (34)
(34)
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 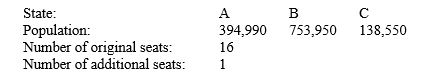
(Multiple Choice)
4.8/5  (26)
(26)
Showing 21 - 40 of 52
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)