Exam 8: Confidence Interval Estimation

TABLE 8-13 A sales and marketing management magazine conducted a survey on salespeople cheating on their expense reports and other unethical conduct. In the survey on 200 managers, 58% of the managers have caught salespeople cheating on an expense report, 50% have caught salespeople working a second job on company time, 22% have caught salespeople listing a "strip bar" as a restaurant on an expense report, and 19% have caught salespeople giving a kickback to a customer. -Referring to Table 8-13, it is possible that the 95% confidence interval calculated from the data will not contain the sample proportion of managers who have caught salespeople cheating on an expense report.

TABLE 8-8 The president of a university would like to estimate the proportion of the student population who owns a personal computer. In a sample of 500 students, 417 own a personal computer. -Referring to Table 8-8, the parameter of interest is the proportion of student population who own a personal computer.

The t distribution is used to develop a confidence interval estimate of the population proportion when the population standard deviation is unknown.

Holding the level of confidence fixed, increasing the sample size will lead to a wider confidence interval.

The t distribution

TABLE 8-8 The president of a university would like to estimate the proportion of the student population who owns a personal computer. In a sample of 500 students, 417 own a personal computer. -Referring to Table 8-8, the parameter of interest is the mean number of students in the population who own a personal computer.

TABLE 8-13 A sales and marketing management magazine conducted a survey on salespeople cheating on their expense reports and other unethical conduct. In the survey on 200 managers, 58% of the managers have caught salespeople cheating on an expense report, 50% have caught salespeople working a second job on company time, 22% have caught salespeople listing a "strip bar" as a restaurant on an expense report, and 19% have caught salespeople giving a kickback to a customer. -Referring to Table 8-13, the sampling error of a 95% confidence interval estimate of the population proportion of managers who have caught salespeople giving a kickback to a customer is ________.

TABLE 8-11 A university wanted to find out the percentage of students who felt comfortable reporting cheating by their fellow students. A surveyed of 2,800 students was conducted and the students were asked if they felt comfortable reporting cheating by their fellow students. The results were 1,344 answered "Yes" and 1,456 answered "no." -Referring to Table 8-11, a 99% confidence interval for the proportion of the student population who feel comfortable reporting cheating by their fellow students is from ________ to ________.

TABLE 8-5 A sample of salary offers (in thousands of dollars) given to management majors is: 48, 51, 46, 52, 47, 48, 47, 50, 51, and 59. Using this data to obtain a 95% confidence interval resulted in an interval from 47.19 to 52.61. -Referring to Table 8-5, it is possible that the mean of the population is not between 47.19 and 52.61.

TABLE 8-8 The president of a university would like to estimate the proportion of the student population who owns a personal computer. In a sample of 500 students, 417 own a personal computer. -Referring to Table 8-8, it is possible that the 99% confidence interval calculated from the data will not contain the sample proportion of students who own a personal computer.

The width of a confidence interval estimate for a proportion will be

The difference between the sample size and the population size is called the sampling error.

An economist is interested in studying the incomes of consumers in a particular region. The population standard deviation is known to be $1,000. A random sample of 50 individuals resulted in an average income of $15,000. What is the upper end point in a 99% confidence interval for the average income?

The confidence interval estimate of the population mean is constructed around the sample mean.

TABLE 8-2 A quality control engineer is interested in the mean length of sheet insulation being cut automatically by machine. The desired length of the insulation is 12 feet. It is known that the standard deviation in the cutting length is 0.15 feet. A sample of 70 cut sheets yields a mean length of 12.14 feet. This sample will be used to obtain a 99% confidence interval for the mean length cut by machine. -Referring to Table 8-2, suppose the engineer had decided to estimate the mean length to within 0.03 with 99% confidence. Then the sample size would be ________.

The t distribution is used to develop a confidence interval estimate of the population mean when the population standard deviation is unknown.

If you were constructing a 99% confidence interval of the population mean based on a sample of n=25 where the standard deviation of the sample s = 0.05, the critical value of t will be

Suppose a 95% confidence interval for μ turns out to be (1,000, 2,100). To make more useful inferences from the data, it is desired to reduce the width of the confidence interval. Which of the following will result in a reduced interval width?

TABLE 8-13 A sales and marketing management magazine conducted a survey on salespeople cheating on their expense reports and other unethical conduct. In the survey on 200 managers, 58% of the managers have caught salespeople cheating on an expense report, 50% have caught salespeople working a second job on company time, 22% have caught salespeople listing a "strip bar" as a restaurant on an expense report, and 19% have caught salespeople giving a kickback to a customer. -Referring to Table 8-13, construct a 95% confidence interval estimate of the population proportion of managers who have caught salespeople giving a kickback to a customer.

As an aid to the establishment of personnel requirements, the director of a hospital wishes to estimate the mean number of people who are admitted to the emergency room during a 24-hour period. The director randomly selects 64 different 24-hour periods and determines the number of admissions for each. For this sample, 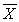= 19.8 and S² = 25. Estimate the mean number of admissions per 24-hour period with a 95% confidence interval.