Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
A dredger scoops a shovel full of mud weighing 4000 pounds from the bottom of a river at a constant rate. Water leaks out uniformly at such a rate that half the weight of the contents is lost when the scoop has been lifted 25 feet. How much work is done by the dredger in lifting the mud this distance?
(Essay)
4.7/5  (42)
(42)
Use cylindrical shells to find the volume of the solid that results when the area of the region enclosed by 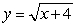 , x = 0, y = 0, and x = 5 is revolved about the y-axis.
, x = 0, y = 0, and x = 5 is revolved about the y-axis.
(Essay)
4.7/5  (32)
(32)
Find the Mass of a lamina bounded by the y-axis and the graph of x = 81 - y4. The density of the lamina is 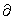 = 3.
= 3.
(Multiple Choice)
4.9/5  (42)
(42)
Approximate the area of the surface generated by revolving the curve y = 3 cos x, 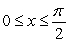 , about the x-axis. Approximate area to three decimal places.
, about the x-axis. Approximate area to three decimal places.
(Multiple Choice)
4.9/5  (32)
(32)
A swimming pool is 24 feet long and 16 feet wide. The bottom is flat but inclined as shown in the figure. The water is 12 feet deep on one end and 2 feet deep on the other. Find the force on the bottom of the pool when it is filled with water (weight density 62.4 lbs/ft3). 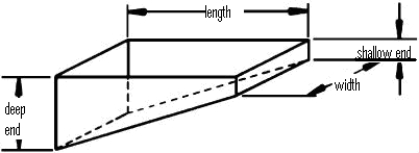
(Essay)
4.9/5  (40)
(40)
Use the method of washers to find the volume of the solid that results when the area of the region enclosed by 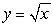 , y = 0, and x = 16 is revolved about the y axis.
, y = 0, and x = 16 is revolved about the y axis.
(Essay)
4.7/5  (30)
(30)
Find the area of the region enclosed by the curves y = 2x2 and y = 2x by integrating with respect to x. Approximate area to three decimal places.
(Multiple Choice)
4.7/5  (33)
(33)
A force of 7x lb is applied to an object as it moves from x = 3 ft to x = 4 ft. How much work is done?
(Essay)
4.8/5  (38)
(38)
Find the work done when a variable force of 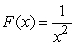 N in the positive x-direction moves an object from x = 4 m to x = 10 m.
N in the positive x-direction moves an object from x = 4 m to x = 10 m.
(Short Answer)
4.9/5  (31)
(31)
Find the area between the curves y = |x - 4|, 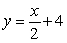 . Approximate area to three decimal places.
. Approximate area to three decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Use a graphing utility to find the area of the region enclosed by the curves y = x2 + 6, y = 1, x = 2, x = 5.
(Essay)
4.9/5  (28)
(28)
Use the Theorem of Pappus to find the volume of the solid that is generated when the region enclosed by y = 1 + x and 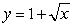 is rotated about the x-axis.
is rotated about the x-axis.
(Essay)
4.9/5  (39)
(39)
Use cylindrical shells to find the volume of the hemisphere that results when the region in the first quadrant enclosed by the circle x2 + y2 = 25 is revolved about the x-axis.
(Essay)
4.9/5  (31)
(31)
Answer true or false: A right-circular cylinder of radius 8cm contains a hollow sphere of radius 7 cm. If the cylinder is filled to a height h with water and the sphere floats so that its highest point is 4cm above the water level, there is 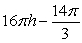 cm3 of water in the cylinder.
cm3 of water in the cylinder.
(True/False)
4.7/5  (27)
(27)
Showing 121 - 140 of 314
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)