Exam 14: Multiple Integrals
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use a triple integral to find the volume of the tetrahedron enclosed by 10x + 10y + z = 2 and the coordinate planes.
(Essay)
4.8/5  (30)
(30)
Find the surface area of the portion of the cone 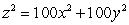 that is above the region in the first quadrant bounded by the line
that is above the region in the first quadrant bounded by the line 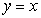 , and the parabola
, and the parabola 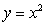 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid in the first octant enclosed by x2 + y2 = 25, y = z, and z = 0.
(Short Answer)
4.9/5  (24)
(24)
Find the volume of the solid bounded by ![Find the volume of the solid bounded by and the rectangle R = [0, 2] * [0, 2].](https://storage.examlex.com/TB6988/11ead0bc_8dab_d8b6_99a0_5373a61db348_TB6988_11.jpg) and the rectangle R = [0, 2] * [0, 2].
and the rectangle R = [0, 2] * [0, 2].
(Multiple Choice)
4.9/5  (28)
(28)
Find the volume of the solid that is enclosed by z = 5(x2 + y2), y = 2x, y = x2, and z = 0.
(Short Answer)
4.7/5  (39)
(39)
Use a triple integral to find the volume of the solid in the first octant enclosed by
z = x2 + y2, y = x, and x = 1.
(Essay)
4.9/5  (37)
(37)
The centroid of a rectangular solid in the first octant with vertices (0, 0, 0), (0, 11, 0), and (11, 0, 11) is
(Multiple Choice)
4.9/5  (41)
(41)
Find 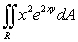 where R is the region in the first quadrant enclosed between
where R is the region in the first quadrant enclosed between 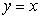 ,
, 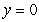 , and x = 1.
, and x = 1.
(Multiple Choice)
4.9/5  (36)
(36)
Use a double integral in polar coordinates to find the volume enclosed by z = 0,
x + 2y - z = -4, and the cylinder x2 + y2 = 1.
(Essay)
4.7/5  (31)
(31)
Find the volume of the solid in the first octant enclosed by 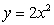 , z = 0, y = 8, x = 0, and x - y + 2z = 2.
, z = 0, y = 8, x = 0, and x - y + 2z = 2.
(Short Answer)
4.7/5  (36)
(36)
Use an appropriate transform to find the area of the region in the first quadrant enclosed by x + y = 1, x + y = 2, 3x - 2y = 2, and 3x - 2y = 5.
(Essay)
4.8/5  (42)
(42)
A lamina with density (x, y) = 2x2 + y2 is bounded by x = y, x = 0, y = 0, y = 2. Find its moment of inertia about the x-axis.
(Multiple Choice)
4.9/5  (38)
(38)
Find the centroid of the lamina enclosed by y = x2 and the line y = 4.
(Essay)
4.8/5  (34)
(34)
Showing 81 - 100 of 117
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)