Exam 25: Population Genetics
Evolutionary biologists usually define population size using the effective population size rather than the census number. What is the effective population size and what factors can affect it?
The effective population size (Ne) is a measure used by evolutionary biologists to estimate the genetic diversity and potential for evolutionary change within a population. It is defined as the size of an idealized population that would lose genetic diversity at the same rate as the actual population under consideration.
Factors that can affect the effective population size include:
1. Genetic drift: Random changes in allele frequencies due to sampling error in small populations can reduce genetic diversity and decrease the effective population size.
2. Population structure: If a population is subdivided into smaller, isolated subpopulations, the effective population size may be smaller than the census number due to limited gene flow between subpopulations.
3. Non-random mating: Inbreeding and assortative mating can reduce genetic diversity and lower the effective population size.
4. Selection: Natural selection can reduce genetic diversity by favoring certain alleles, leading to a decrease in effective population size.
5. Mutation: New mutations can increase genetic diversity, but the rate of mutation and the effects of selection on new mutations can also impact the effective population size.
6. Population bottlenecks: Events that cause a drastic reduction in population size, such as natural disasters or human activities, can lead to a decrease in genetic diversity and a smaller effective population size.
Overall, the effective population size provides a more accurate measure of the genetic potential and evolutionary dynamics of a population compared to the simple census number. Understanding the factors that can affect the effective population size is crucial for conservation efforts and for predicting the long-term viability of populations.
A newspaper story on AIDS reports that an allele (R) confers complete resistance to HIV when homozygous and that 1% of the human population is resistant (RR). The story also states that 20% of the population carries one copy of the resistance allele (i.e., is heterozygous). Is this a guess, an approximation, or an exact frequency, assuming that the population is at Hardy-Weinberg equilibrium?
The Hardy-Weinberg principle provides a mathematical model to study genetic variation in a population under a set of assumptions, including random mating, no mutation, no migration, no selection, and a large population size. According to this principle, allele and genotype frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences.
The principle also gives us the Hardy-Weinberg equation, which for a gene with two alleles (R and r) is:
p² + 2pq + q² = 1
where:
- p is the frequency of one allele (R in this case),
- q is the frequency of the other allele (r),
- p² is the frequency of the homozygous genotype (RR),
- 2pq is the frequency of the heterozygous genotype (Rr),
- q² is the frequency of the other homozygous genotype (rr).
Given the information from the newspaper story:
- p² (the frequency of the homozygous resistant genotype, RR) is 1% or 0.01,
- 2pq (the frequency of the heterozygous genotype, Rr) is 20% or 0.20.
We can use the first piece of information to solve for p:
p² = 0.01
p = √0.01
p = 0.1
Now, we can use the value of p to find q:
p + q = 1
0.1 + q = 1
q = 0.9
Now we can check if the given frequency for the heterozygous genotype (2pq) is correct:
2pq = 2 * 0.1 * 0.9
2pq = 0.18
The calculated frequency of the heterozygous genotype (Rr) is 18%, not 20% as stated in the newspaper story. Therefore, the reported frequency of 20% for the heterozygous genotype is not exact if the population is at Hardy-Weinberg equilibrium. It could be an approximation or a guess, or it could indicate that the population is not in Hardy-Weinberg equilibrium due to one of the evolutionary forces such as selection, mutation, non-random mating, genetic drift, or gene flow affecting the population.
A new kind of tulip is produced that develops only purple or pink flowers. Assume that flower color is controlled by a single-gene locus and that the purple allele (C) is dominant to the pink allele (c). A random sample of 1000 tulips from a large cultivated field yields 847 purple flowers and 153 pink flowers.
a. Determine the frequency of the purple and pink alleles in this field population.
b. Estimate the proportion of all purple flowering plants that are heterozygotes and homozygotes.
a. Determine the frequency of the purple and pink alleles in this field population.
To determine the frequency of the purple and pink alleles, we can use the Hardy-Weinberg principle, which states that the allele frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences. According to this principle, the frequency of the two alleles should add up to 1 (or 100%).
Let p be the frequency of the dominant purple allele (C), and q be the frequency of the recessive pink allele (c). The Hardy-Weinberg principle also states that the genotype frequencies in the population can be represented as p^2 for the homozygous dominant (CC), 2pq for the heterozygous (Cc), and q^2 for the homozygous recessive (cc).
Given that we have 153 pink flowering plants, which are homozygous recessive (cc), we can calculate the frequency of the recessive allele (q^2) as follows:
q^2 = number of pink flowering plants / total number of plants
q^2 = 153 / 1000
q^2 = 0.153
To find q, we take the square root of q^2:
q = √0.153
q ≈ 0.391
Now, since p + q = 1, we can calculate p:
p = 1 - q
p = 1 - 0.391
p ≈ 0.609
Therefore, the frequency of the dominant purple allele (C) is approximately 0.609, and the frequency of the recessive pink allele (c) is approximately 0.391 in the field population.
b. Estimate the proportion of all purple flowering plants that are heterozygotes and homozygotes.
We know that the purple flowering plants can be either homozygous dominant (CC) or heterozygous (Cc). To find the proportion of each, we use the Hardy-Weinberg genotype frequencies:
The proportion of homozygous dominant (CC) is p^2:
p^2 = (0.609)^2
p^2 ≈ 0.371
The proportion of heterozygous (Cc) is 2pq:
2pq = 2 * (0.609) * (0.391)
2pq ≈ 0.476
Since the total number of purple flowering plants is 847, we can calculate the estimated number of each genotype:
Homozygous dominant (CC) = p^2 * total purple plants
Homozygous dominant (CC) ≈ 0.371 * 847
Homozygous dominant (CC) ≈ 314
Heterozygous (Cc) = 2pq * total purple plants
Heterozygous (Cc) ≈ 0.476 * 847
Heterozygous (Cc) ≈ 403
Therefore, out of the 847 purple flowering plants, approximately 314 are estimated to be homozygous dominant (CC), and approximately 403 are estimated to be heterozygous (Cc). Note that due to rounding, these numbers may not add up exactly to 847.
_____ increases the frequency of homozygotes in a population compared to the results of random mating.
The Hardy-Weinberg law (equation) is a mathematical model in which allelic frequencies in populations remain constant from generation to generation. Given all the conditions that must be met for the Hardy-Weinberg equation to be valid, why is this equation useful for studying population genetics?
Which agent of evolution is most likely responsible for the decrease in the frequency of a recessive allele as shown in the accompanying below? 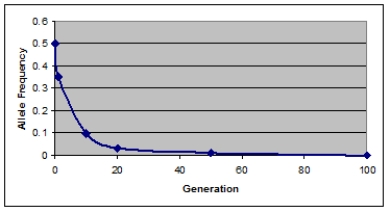
You are studying a single-gene locus with two alleles in a population that is in Hardy-Weinberg equilibrium. Examination of a large sample of individuals from the population reveals there are six times as many heterozygotes as there are homozygote recessive individuals in this population. What is the frequency of the recessive allele?
Suppose a disease is caused by a recessive allele. Individuals with the disease produce only about 60% of the offspring of individuals with the normal phenotype. The mutation rate from the dominant to the recessive allele is 1 × 10-5. At mutation-selection equilibrium, what will be the frequency of the recessive allele?
If there is random mating in a population and no evolutionary forces are acting on the population, what will be the expected outcome?
_____ is when the heterozygote has a higher fitness than either of the two homozygotes (W11 < W12 > W22). Allelic frequencies will change in this population until _____.
_____ ultimately produces all new genetic variation in a population.
Human blood type is determined by three alleles IA, IB, and IO. The alleles IA and IB are co-dominant to each other, and both are dominant to IO. Within a large, randomly mating population (540,000 individuals), the frequencies for the blood type alleles are 0.3 for the IA allele, 0.6 for the IO allele, and 0.1 for the IB allele.
a. Calculate the expected numbers of people in the population having each of the blood types A, B, AB, and O.
b. Determine the percentage of type B people that are heterozygotes (IBIO).
Huntington's disease is caused by a single dominant allele and results in progressive mental and neurological damage. The disease usually becomes symptomatic when a person is between 30 and 50 years old and the patient usually dies within 15 years of diagnosis. Approximately 1 in 25,000 Caucasians have this disease. Huntington's disease has not been associated with any other disease, now or in the past. Why might natural selection not have eliminated such a deleterious allele from the population?
By the early 1980s, the population of Florida panthers had dwindled to fewer than 30. Furthermore, within this population was a high frequency of detrimental traits, including low sperm count and undescended testicles in males and kinked tails in both sexes. The future for this iconic population was bleak at best. Provide an explanation for the observed detrimental traits. Provide a possible solution that would both increase the likelihood that the population would survive and preserve the genetic identity of this unique population.
Use Figure 25.3 to determine the BEST answers for the following question. 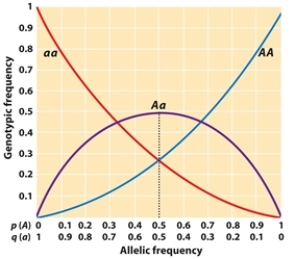 -When a population is in Hardy-Weinberg equilibrium, what is the significance of two alleles with equal frequencies (p = q = 0.5)?
-When a population is in Hardy-Weinberg equilibrium, what is the significance of two alleles with equal frequencies (p = q = 0.5)?
Use Figure 25.3 to determine the BEST answers for the following question. 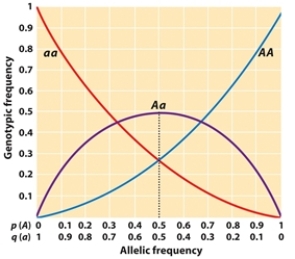 -When a population is in Hardy-Weinberg equilibrium, what is the approximate frequency of the aa homozygote and the Aa heterozygote when the frequency of AA is approximately 0.5?
-When a population is in Hardy-Weinberg equilibrium, what is the approximate frequency of the aa homozygote and the Aa heterozygote when the frequency of AA is approximately 0.5?
Through _____, alleles may disappear from a population simply by chance.
Rapid changes in allelic frequencies by _____ take place in populations that are small.
Explain how inbreeding can have a positive effect on population fitness.
Suppose that in a population the frequency of a particular recessive condition is 1/400. Assume the presence of only a dominant allele (A) and a recessive allele (a) in the population and that the population is at Hardy-Weinberg equilibrium. What is the frequency of the recessive allele that causes the condition?
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)