Exam 7: Goal Programming and Multiple Objective Optimization

Suppose that the first goal in a GP problem is to make 3 X₁ + 4 X₂ approximately equal to 36. Using the deviational variables d₁^- and d₁⁺, what constraint can be used to express this goal?

Exhibit 7.2 The following questions are based on the problem below. An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel. A 1 Problem data 2 Expected retun 12\% 10\% 3 Risk rating 0.50 0.20 4 5 Variables Tatal 6 Amount invested 0 0 0 7 Minimum required \ 10,000 \ 15,000 \ 150,000 8 9 Objectives: 10 Average return 0 11 Average risk 0 -Refer to Exhibit 7.2. Which cell(s) is(are) the target cells in this model?

A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000. Based on the following formulation and associated integer solution, what values should go in cells B2:E16 of the spreadsheet? 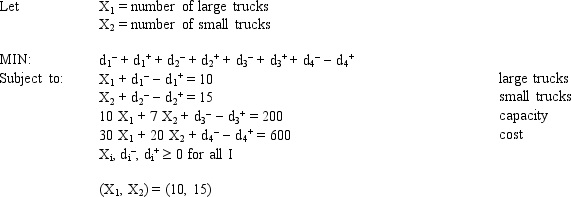A B C D E 1 Problem Data Large Small 2 Cost 3 Capacity 4 5 Goal Constraints Large Small Cost Capacity 6 Actual Amount 7 + Under 8 - Over 9 = Goal 10 Target Value 11 12 Weights 13 Under 14 Over 15 16 Objective

Exhibit 7.4 The following questions are based on the problem below. Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below: Truck Weight Capacity Box Capacity Cast per pound 1 800 pounds 5 \ 0.34 2 900 pounds 6 \ 0.42 3 700 pounds 4 \ 0.25 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight. The following integer goal programming formulation applies to his problem. Y₁ = weight loaded in truck 1; Y₂ = weight loaded in truck 2; Y₃ = weight loaded in truck 3; X_i,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions. 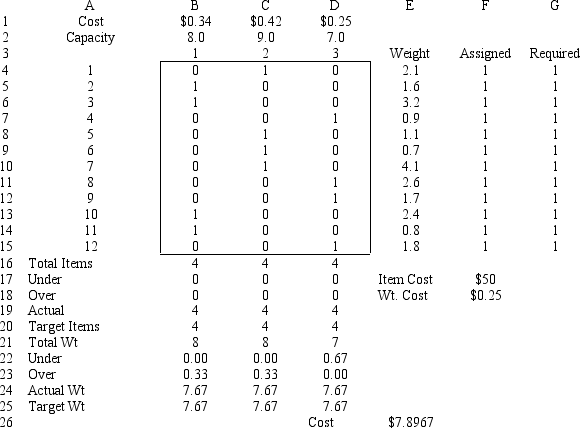-Refer to Exhibit 7.4. The solution indicates Truck 3 is under the target weight by 67 pounds. What if anything can be done to this model to provide a solution in which Truck 3 is closer to the target weight?

Exhibit 7.3 The following questions are based on the problem below. An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel. 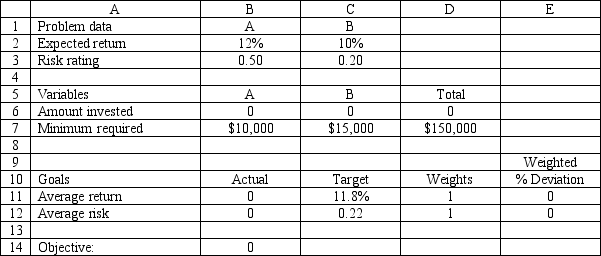-Refer to Exhibit 7.3. What formula goes in cell E11?

The primary benefit of a MINIMAX objective function is

The MINIMAX objective

Exhibit 7.1 The following questions are based on the problem below. A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet. 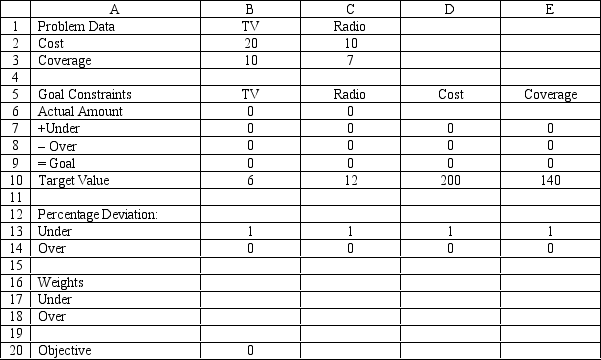-Refer to Exhibit 7.1. What formula goes in cell D6?

Exhibit 7.1 The following questions are based on the problem below. A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet. -Refer to Exhibit 7.1. If the company is very concerned about going over the $200,000 budget, which cell value should change and how should it change?

A dietician wants to formulate a low cost, high calorie food product for a customer. The following information is available about the 2 ingredients which can be combined to make the food. The customer wants 1000 pounds of the food product and it must contain at least 250 pounds of Food 1 and 300 pounds of Food 2. Faod 1 Faod 2 Requirements Cost (\ / pound 1.00 1.25 Minimize \% Fat 15 25 Less than 30\% \% Protein 35 40 At least 37\% \% Carbahydrate 50 35 At least 40\% Calorieshpound 3000 2000 Maximize Mrrimum pounds of food 250 300 Formulate the MOLP for this problem.

Which of the following is true regarding goal programming?

Goal programming solution feedback indicates that the d₄⁺ level of 50 should not be exceeded in future solution iterations. How should you modify your goal constraint 40 X₁ + 20 X₂ + d₄^ + d₄⁺ = 300 To accommodate this requirement?

A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000. Formulate a goal programming model of this problem.

Which of the following is false regarding a goal constraint?

Exhibit 7.4 The following questions are based on the problem below. Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below: Truck Weight Capacity Box Capacity Cast per pound 1 800 pounds 5 \ 0.34 2 900 pounds 6 \ 0.42 3 700 pounds 4 \ 0.25 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight. The following integer goal programming formulation applies to his problem. Y₁ = weight loaded in truck 1; Y₂ = weight loaded in truck 2; Y₃ = weight loaded in truck 3; X_i,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions. -Refer to Exhibit 7.4. Given the solution indicated in the spreadsheet, which trucks, if any, are under an equal weight amount, and which trucks are over an equal weight amount?

What is the soft constraint form of the following hard constraint? 3X₁ + 2 X₂  10

The d_i⁺, d_i^-variables are referred to as

Exhibit 7.3 The following questions are based on the problem below. An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel. -Refer to Exhibit 7.3. Which value should the investor change, and in what direction, if he wants to reduce the risk of the portfolio?

An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are: Fund Rate of return Risk Minimum investment 12\% 0.5 \ 20,000 9\% 0.3 \ 10.000 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32. The following Excel spreadsheet has been created to solve a goal programming problem with a MINIMAX objective based on the following goal programming formulation with MINIMAX objective and corresponding solution. 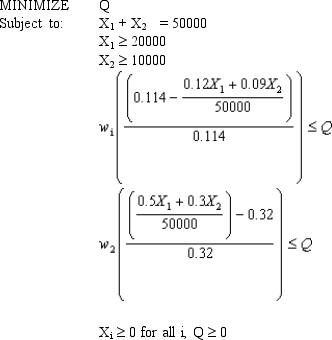with solution (X₁, X₂) = (15,370, 34,630). What values should go in cells B2:D14 of the spreadsheet? A 1 Problem deta 2 Expected return 3 Risk rating 4 5 Variables A Total 6 Amount invested 7 Minimum required 8 9 Weighted 10 Goals Actual Target Weights \% Devintion 11 Average retun 1 12 Average risk 1 13 14 Objective: