Exam 3: Modeling and Solving Lp Problems in a Spreadsheet
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
Using Data Envelopment Analysis (DEA) for an inefficient unit, a more efficient composite unit can be found by
Free
(Multiple Choice)
4.9/5  (44)
(44)
Correct Answer:
C
The "Analyze Without Solving" tool in Risk Solver Platform (RSP) is useful for
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
A
A company needs to purchase several new machines to meet its future production needs. It can purchase three different types of machines A, B, and C. Each machine A costs $80,000 and requires 2,000 square feet of floor space. Each machine B costs $50,000 and requires 3,000 square feet of floor space. Each machine C costs $40,000 and requires 5,000 square feet of floor space. The machines can produce 200, 250 and 350 units per day respectively. The plant can only afford $500,000 for all the machines and has at most 20,000 square feet of room for the machines. The company wants to buy as many machines as possible to maximize daily production.
What are the key formulas for this Excel spreadsheet implementation of the following formulation?
Let mumber of machines of type i purchased
MAX: 200+250+300 Subject to: 2+3+5\leq20 80+50+40\leq500 ,\geq0
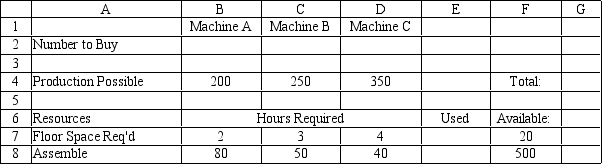
Free
(Essay)
4.9/5  (43)
(43)
Correct Answer:
Exhibit 3.2
The following questions are based on this problem and accompanying Excel windows.
The Byte computer company produces two models of computers, Plain and Fancy. It wants to plan how many computers to produce next month to maximize profits. Producing these computers requires wiring, assembly and inspection time. Each computer produces a certain level of profits but faces only a limited demand. There are also a limited number of wiring, assembly and inspection hours available in each month. The data for this problem is summarized in the following table.
Let Number of Plain computers to produce
Number of Fancy computers to produce
MAX:
Subject to: (wiring hours)
(assembly hours)
(inspection hours)
(Plin computers demand)
(Fancy computers demand)
A B C D E 1 Byte Computer Company 2 3 Plain Fancy 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Used Available 8 Wiring 0.4 0.5 50 9 Assembly 0.5 0.4 50 10 Inspection 0.2 0.3 22 11 Plain Demand 1 80 12 Fancy Demand 1 90
-Refer to Exhibit 3.2. Which cells should be the constraint cells in this problem?
(Multiple Choice)
4.7/5  (36)
(36)
Exhibit 3.2
The following questions are based on this problem and accompanying Excel windows.
The Byte computer company produces two models of computers, Plain and Fancy. It wants to plan how many computers to produce next month to maximize profits. Producing these computers requires wiring, assembly and inspection time. Each computer produces a certain level of profits but faces only a limited demand. There are also a limited number of wiring, assembly and inspection hours available in each month. The data for this problem is summarized in the following table.
Let Number of Plain computers to produce
Number of Fancy computers to produce
MAX:
Subject to: (wiring hours)
(assembly hours)
(inspection hours)
(Plin computers demand)
(Fancy computers demand)
A B C D E 1 Byte Computer Company 2 3 Plain Fancy 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Used Available 8 Wiring 0.4 0.5 50 9 Assembly 0.5 0.4 50 10 Inspection 0.2 0.3 22 11 Plain Demand 1 80 12 Fancy Demand 1 90
-Refer to Exhibit 3.2. What formula should be entered in cell E5 in the accompanying Excel spreadsheet to compute total profit?
(Multiple Choice)
4.9/5  (46)
(46)
Exhibit 3.3
The following questions are based on this problem and accompanying Excel windows.
Jack's distillery blends scotches for local bars and saloons. One of his customers has requested a special blend of scotch targeted as a bar scotch. The customer wants the blend to involve two scotch products, call them A and B. Product A is a higher quality scotch while product B is a cheaper brand. The customer wants to make the claim the blend is closer to high quality than the alternative. The customer wants 50 1500 ml bottles of the blend. Each bottle must contain at least 48% of Product A and at least 500 ml of B. The customer also specified that the blend have an alcohol content of at least 85%. Product A contains 95% alcohol while product B contains 78%. The blend is sold for $12.50 per bottle. Product A costs $7 per liter and product B costs $3 per liter. The company wants to determine the blend that will meet the customer's requirements and maximize profit.
Let Number of liters of product in total blend delivered
Number of liters of product in total blend delivered
MIN:
Subject to: (Total liters of mix)
minimum)
minimum)
(85\% alcohol minimum)
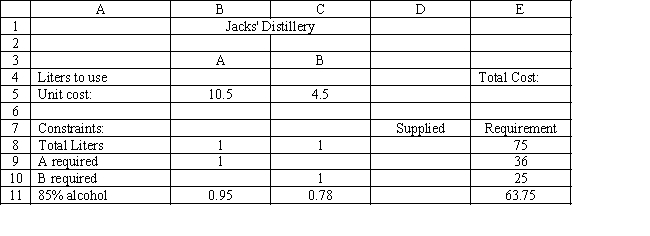 -Refer to Exhibit 3.3. Which cells should be changing cells in this problem?
-Refer to Exhibit 3.3. Which cells should be changing cells in this problem?
(Multiple Choice)
4.9/5  (26)
(26)
What action is required to make Risk Solver Platform (RSP) solve a specified problem?
(Multiple Choice)
4.9/5  (49)
(49)
Exhibit 3.5
The following questions are based on this problem and accompanying Excel windows.
A company is planning production for the next 4 quarters. They want to minimize the cost of production. The production cost is stable but demand and production capacity vary from quarter to quarter. The maximum amount of inventory which can be held is 12,000 units and management wants to keep at least 3,000 units on hand. Quarterly inventory holding cost is 3% of the cost of production. The company estimates the number of units carried in inventory each month by averaging the beginning and ending inventory for each month. There are currently 5,000 units in inventory. The company wants to produce at no less than one half of its maximum capacity in any quarter.
1 2 3 4 Unit Production Cost \ 300 \ 300 \ 300 \ 300 Units Demanded 2,000 9,000 12,000 11,000 Maximum Production 8,000 7,000 8,000 9,000 Let = number of units produced in quarter i,i=1,\ldots,4 = beginning inventory for quarter i MiN: 300+300+300+300+ 9 + /2+9 + /2+9 + /2+9 + /2 Subject to: 4000\leq\leq8000 3500\leq\leq7000 4000\leq\leq8000 4500\leq\leq9000 3000\leq+-2000\leq12000 3000\leq+-9000\leq12000 3000\leq+-12000\leq12000 3000\leq+-11000\leq12000 =+-2000 =+-9000 =+-12000 =+-11000 ,\geq0 A 1 Quarter 2 1 2 3 4 3 Beginning Inventory 5,000 11,000 9,000 5,000 4 Units Produced 8,000 7,000 8,000 9,000 5 Units Demanded 2,000 9,000 12,000 11,000 6 Ending Inventory 11,000 9,000 5,000 3,000 7 8 Minimum Procduction 4,000 3,500 4,000 4,500 9 Maximum Froduction 8,000 7,000 8,000 9,000 10 11 Minimum Inventory 3,000 3,000 3,000 3,000 12 Maximum Inventory 12,000 12,000 12,000 12,000 13 14 Unit Production Cost \ 300 \ 300 \ 300 \ 300 15 Unit Carrying Cost 3.0\% \ 9,00 \ 9.00 \ 9,00 \ 9.00 16 17 Quarterly Production Cost \ 2,400,000 \ 2,100,000 \ 2,400,000 \ 2,700,000 18 Quarterly Carrying Cost \ 72,000 \ 90,000 \ 63,000 \ 36,000 19 20 Tota1 Cost \ 9,861,000
-Refer to Exhibit 3.5. What formula could be entered in cell F20 in the accompanying Excel spreadsheet to compute the Total Cost for all four quarters?
(Multiple Choice)
4.8/5  (30)
(30)
Exhibit 3.1
The following questions are based on this problem and accompanying Excel windows.
Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited, so at most 8 will be produced.
Let
= Number of Beds to produce = Number of Desks to produce The LP model for the problem is
MAX: 30+40 Subject to: 6+4\leq36 (carpentry) 4+8\leq40 (varnishing) \leq8 (demand for desks) ,\geq0 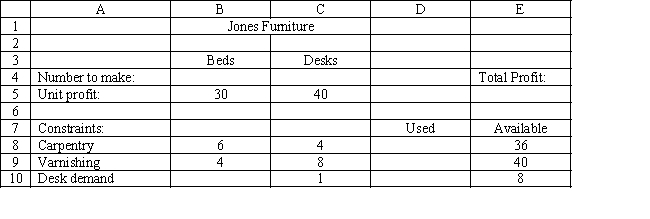 -Refer to Exhibit 3.1. What formula should be entered in cell D8 in the accompanying Excel spreadsheet to compute the amount of carpentry used?
-Refer to Exhibit 3.1. What formula should be entered in cell D8 in the accompanying Excel spreadsheet to compute the amount of carpentry used?
(Multiple Choice)
4.9/5  (36)
(36)
A company needs to purchase several new machines to meet its future production needs. It can purchase three different types of machines A, B, and C. Each machine A costs $80,000 and requires 2,000 square feet of floor space. Each machine B costs $50,000 and requires 3,000 square feet of floor space. Each machine C costs $40,000 and requires 5,000 square feet of floor space. The machines can produce 200, 250 and 350 units per day respectively. The plant can only afford $500,000 for all the machines and has at most 20,000 square feet of room for the machines. The company wants to buy as many machines as possible to maximize daily production.
Formulate the LP for this problem.
(Essay)
4.9/5  (29)
(29)
You have been given the following linear programming model and Excel spreadsheet to solve this problem. What formulas should be entered into cells E5 and D8:D10 to implement this model?
MAX: 4+3 Subject to: 6+7\leq84 \leq10 \leq8 ,\geq0 A B C D E 1 2 3 4 Number to make: OBJ. FN. VALUE 5 Unit profit: 4 3 6 7 Constraints: Used Available 8 1 6 7 84 9 2 1 0 10 10 3 0 1 8
(Essay)
4.9/5  (33)
(33)
A hospital needs to determine how many nurses to hire to cover a 24 hour period. The nurses must work 8 consecutive hours but can start work at the start of 6 different shifts. They are paid different wages depending on when they start their shifts. The number of nurses required per 4-hour time period and their wages are shown in the following table.
Time period Required \# of Nurses Wage (\ /) 12-4 20 15 4-8 30 16 am 8-12 40 13 12-4 50 13 4-4 40 14 8-12 30 15
What values would you enter in the Risk Solver Platform (RSP) task pane for the following cells for this Excel spreadsheet implementation of the formulation for this problem?
Objective Cell:
Variables Cells:
Constraints Cells:
Let mumber of nurses warking in thme period
MiN: 1+1+1+1+1+1 Subject ta: 1+1\geq30 1+1\geq40 1+1\geq50 1+1\geq40 1+1\geq30 1+1\geq20 \geq0 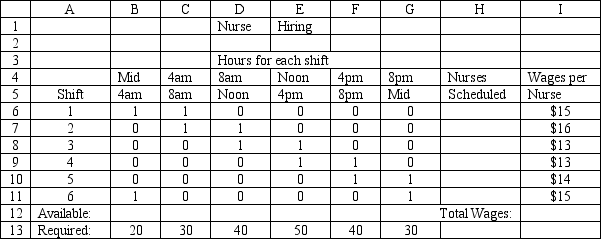
(Essay)
4.8/5  (34)
(34)
Data Envelopment Analysis (DEA) is an LP-based methodology in which weighted sums of inputs and outputs are calculated and
(Multiple Choice)
4.8/5  (31)
(31)
You have been given the following linear programming model and Excel spreadsheet to solve this problem. What numbers should be entered into cells B5:C5 and B8:C10 to implement this model?
MIN:
Subject to:
8+5\geq80 3+5\geq60 ,\geq0 A B C D E 1 2 3 4 Number to make: OBJ. FN. VALUE 5 Unit profit: 6 7 Constraints: Used Available 8 1 8 9 2 80 10 3 60
(Essay)
4.9/5  (29)
(29)
The built-in Solver in Excel is found under which tab on the ribbon?
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)