Exam 8: Nonlinear Programming and Evolutionary Optimization
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
A B C D E 1 Length Width Stories Parking 2 108.39492 92.255243 6 80,000 3 Max Values 300 300 6 4 5 Total Floor Area 60,000 \geq 60,000 6 Total Lot Area 90,000 = 90,000 7 Min. Parking Area 65,000 \geq 0 8 Max. Bld Height 60 \leq 65 9 10 Cost 11 Height Factor 0.6 Total Height 60 12 Area Factor 0.01 Floor Area 10,000 13 Cost \ 136.0 millions \
-Refer to Exhibit 8.2. What formula would you place in cell D13 to calculate total cost?
The spreadsheet implementation of this formulation applies to the following questions.
A B C D E 1 Length Width Stories Parking 2 108.39492 92.255243 6 80,000 3 Max Values 300 300 6 4 5 Total Floor Area 60,000 \geq 60,000 6 Total Lot Area 90,000 = 90,000 7 Min. Parking Area 65,000 \geq 0 8 Max. Bld Height 60 \leq 65 9 10 Cost 11 Height Factor 0.6 Total Height 60 12 Area Factor 0.01 Floor Area 10,000 13 Cost \ 136.0 millions \
-Refer to Exhibit 8.2. What formula would you place in cell D13 to calculate total cost?
Free
(Short Answer)
4.7/5  (29)
(29)
Correct Answer:
=SUMPRODUCT(B11:B12,D11:D12)
Which point or points are local optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 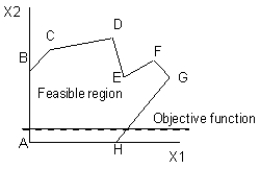
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
D
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formula goes in cell D4 of the spreadsheet? 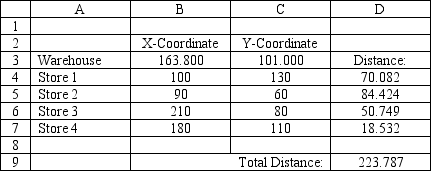
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
C
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
A B C D E 1 Length Width Stories Parking 2 108.39492 92.255243 6 80,000 3 Max Values 300 300 6 4 5 Total Floor Area 60,000 \geq 60,000 6 Total Lot Area 90,000 = 90,000 7 Min. Parking Area 65,000 \geq 0 8 Max. Bld Height 60 \leq 65 9 10 Cost 11 Height Factor 0.6 Total Height 60 12 Area Factor 0.01 Floor Area 10,000 13 Cost \ 136.0 millions \
-Refer to Exhibit 8.2. The company wishes to have a relatively square building. Thus, they wish neither the building length nor the building width exceed the other by more than 25%. Add constraint(s) to enforce this design constraint.
The spreadsheet implementation of this formulation applies to the following questions.
A B C D E 1 Length Width Stories Parking 2 108.39492 92.255243 6 80,000 3 Max Values 300 300 6 4 5 Total Floor Area 60,000 \geq 60,000 6 Total Lot Area 90,000 = 90,000 7 Min. Parking Area 65,000 \geq 0 8 Max. Bld Height 60 \leq 65 9 10 Cost 11 Height Factor 0.6 Total Height 60 12 Area Factor 0.01 Floor Area 10,000 13 Cost \ 136.0 millions \
-Refer to Exhibit 8.2. The company wishes to have a relatively square building. Thus, they wish neither the building length nor the building width exceed the other by more than 25%. Add constraint(s) to enforce this design constraint.
(Essay)
4.8/5  (42)
(42)
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%, compounded quarterly, on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income. What constraint must be entered in the Risk Solver Platform (RSP) task pane? 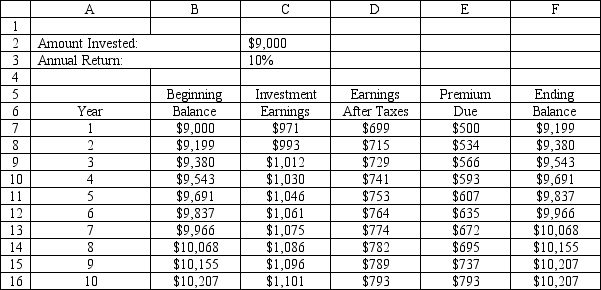
(Multiple Choice)
4.8/5  (35)
(35)
An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. The following spreadsheet has been set up to solve the problem. What formula goes in cell B11 in this problem? A 1 2 3 Annual Demand: 20,000 4 5 Cost per Unit: \ 25 6 Ordering Cost: \ 30 7 Carrying Cust: 25\% 8 9 Order Quantity: 483.73 10 11 Total Cost: \ 502,738.61
(Multiple Choice)
4.8/5  (39)
(39)
The Reduced Gradient is similar to which of these terms from linear programming?
(Multiple Choice)
4.9/5  (35)
(35)
What is the straight line (Euclidean) distance between the points (5,7) and (1, 11)?
(Multiple Choice)
4.8/5  (29)
(29)
Which point or points are global optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 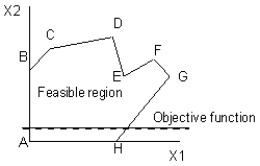
(Multiple Choice)
4.7/5  (36)
(36)
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formula goes in cell D9 of the spreadsheet? 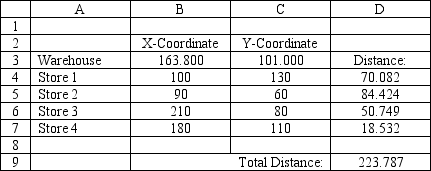
(Multiple Choice)
4.8/5  (43)
(43)
The main difference between LP and NLP problems is that NLPs will have a
(Multiple Choice)
4.9/5  (37)
(37)
How much are additional units of Labor worth based on the following sensitivity report?
Final Rediuced Cell Name Value Gradient \ B\ 4 Number to make: 9.42 0 \ \ 4 Number to make: 1.71 0
Final Lagrange Cell Name Value Multiplier \ \ 8 Wood 42 0 \ \ 9 Labor 132 1.21 \ \ 10 Plywood 24 2.57
(Multiple Choice)
4.9/5  (39)
(39)
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. Which cell(s) in the spreadsheet represent the decision variables in the problem? 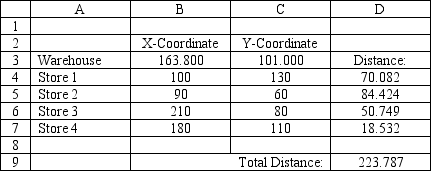
(Multiple Choice)
4.8/5  (30)
(30)
When using the GRG algorithm to solve NLPs one should try multiple starting points because
(Multiple Choice)
4.8/5  (29)
(29)
A company wants to locate a new warehouse to minimize the distance travelled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formulas should go in cells D4:D9 of the spreadsheet for this problem?
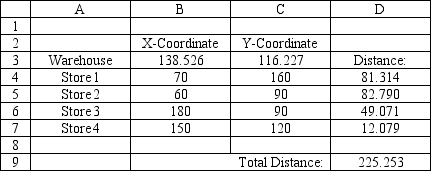
(Essay)
4.8/5  (29)
(29)
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $12,000 and hopes he can earn 18% on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income.
If the Risk Solver Platform (RSP) is used, which are the Objective, Variables and Constraint cells in the spreadsheet for this problem?
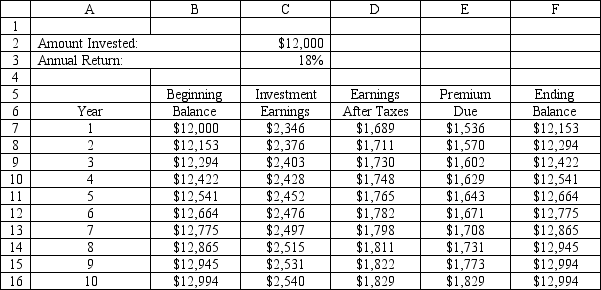
(Essay)
4.9/5  (35)
(35)
A construction company just purchased a 300 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
Formulate the NLP for the problem.
(Essay)
4.8/5  (36)
(36)
The Sweet Water beverage company is designing a new soft drink can. The designers wish to minimize the manufacturing cost of the can, a cost that is directly related to the amount of aluminum used in the can. The can must hold at least 350 ml (or cm3) of beverage, have a diameter between 3 and 7 cm, and have a height between 7 and 19 cm.
Formulate the NLP for Sweet Water.
(Essay)
4.9/5  (33)
(33)
A company wants to locate a new warehouse to minimize the longest distance travelled by any of its delivery trucks. It has four stores and their coordinates are listed in the below.
X-Coordinate Y-Coordinate Store 1 70 160 Store 2 60 90 Store 3 180 90 Store 4 150 120
Let X and Y represent the X, Y coordinates of the new warehouse. The NLP for this problem and solution is the following.

(Essay)
4.9/5  (36)
(36)
Showing 1 - 20 of 68
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)