Exam 8: Nonlinear Programming and Evolutionary Optimization
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
The straight line (Euclidean) distance between two points (X1, Y1) and (X2, Y2) is calculated as
(Multiple Choice)
4.9/5  (30)
(30)
The total annual cost for the economic order quantity model is
(Multiple Choice)
4.8/5  (29)
(29)
A company wants to locate a new warehouse to minimize the distance travelled by its delivery trucks. It has four stores and their coordinates are listed in the below.
X-Coordinate Y-Coordinate Store 1 70 160 Store 2 60 90 Store 3 180 90 Store 4 150 120 Formulate the objective function for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
(Essay)
4.8/5  (30)
(30)
An investor is developing a portfolio of stocks. She has identified 3 stocks in which to invest. She wants to earn at least 11% return but with minimum risk.
Let: Pi = proportion of total funds invested in i, i = A, B, C
The NLP for this problem is:
MIN:
Subject to:
++=1 0.1072+0.1068+0.1187\geq0.11 ,,\geq0 ,,\leq1
What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
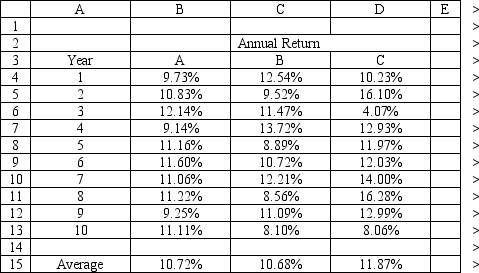
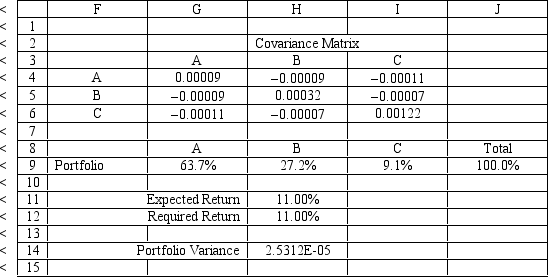
(Essay)
4.8/5  (38)
(38)
The optimal solution to a NLP problem can occur at a(n) I.cormer paint.
II.interior point
(Multiple Choice)
4.9/5  (28)
(28)
Project 8.1 - Truck Company Expansion
Kornfield Trucking handles private and commercial moves. They currently own 500 moving vans and employ 2000 full-time workers. Their trucks are used to pick-up and deliver office and household goods throughout the Eastern and Southeastern states. Kornfield mans each truck with three workers. This allows driver swaps providing increased miles-covered-per-hour ratio while staying within safety requirements for individual driving time. A 3-person crew also reduces company reliance on local help. Local distributors and warehouses provide a pool of laborers for loading and unloading the moving trucks. While in the past this arrangement has worked well, the arrangement has soured recently as the temporary workers have demanded higher wages while produced less work. Despite their pay and benefits package, Kornfield still finds that the nature of the work (lifting and time on the road) makes for a high rate of turnover. Thus, Kornfield maintains an excess of workers/drivers, but no more than 3.75 workers per truck at any time.
The following information is available on the trucks in the Kornfield inventory and their options for new purchases.
Purchase Salvage Value Yearly Maintenance Miles Per Year Miles per Gallon" New Truck \ 55,000 \@cdots 750 100,000 12.5 Old Truck \@cdots \ 25,000 \ 1500 100,000 10 *assume \1 .50/gal The following information applies to Kornfield personnel actions.
Hiring Cost Firing Cost Salary New Worker \ 1000 -- \ 28,000 Old Worker -- \ 1500 \ 35,000 Kornfield has an operating budget of $ 75M next year and wants to expand their operations. As a part of this expansion, they are considering options for their truck fleet and may purchase new trucks, sell old trucks to salvage or some combination of the two. Any salvage money received is rolled into the operating budget. Kornfield is also considering possible changes to their work force. Their current force has a fairly high average salary and their operating budget is not greatly affected by releasing current employees. On the other hand, newer employees carry a much lower average salary and do not tax the operating budget heavily in hiring and training costs.
The Cobb-Douglas production function is used to model the number of vehicle miles driven per year. This function represents the quantity Kornfield management would like to maximize as they expand their operations. The general form of the Cobb-Douglas production function is the following:
where y is the output, each Xi represents an input and the letters represent constants. This function generalizes to fewer or a greater number of parameters than the three depicted above. The constants for the Kornfield Trucking production function are (a, b, c, d) = (9.1, 0.05, 0.40, 0.50).
Formulate the Kornfield Trucking problem as a non-linear programming problem. Implement the problem in Excel and use Risk Solver Platform (RSP) generalized reduced gradient (GRG) routing to obtain a solution to the problem. What is a recommended solution for Kornfield Trucking?
(Essay)
4.9/5  (34)
(34)
An investor is developing a portfolio of stocks. She has identified 3 stocks to invest in. She wants to earn at least 5% return but with minimum risk. The problem data is given in the following Excel spreadsheet. What formula should be entered in cell H11 of the Excel spreadsheet? 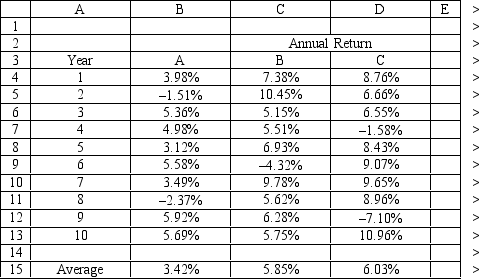
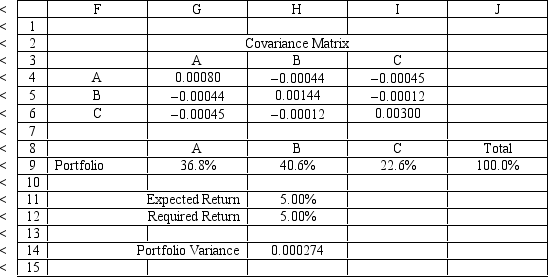
(Multiple Choice)
4.9/5  (34)
(34)
How much must the objective function coefficient of the variable X2 increase before any X2s are produced based on the following sensitivity report?
Final Reduced Cell Name Value Gradient \ B\ 4 Number to make: 9.428 0 \ \ 4 Number to make: 0 -1.96
Final Lagrange Cell Name Value Multiplier \ \ 8 Used 42 0 \ \ 9 Used 132 0.214 \ \ 10 Used 24 1.214
(Short Answer)
4.8/5  (35)
(35)
Showing 61 - 68 of 68
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)