Exam 2: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Solve the inequality and graph the solution on the real number line.
(Multiple Choice)
4.8/5  (41)
(41)
Find all the zeros of the function and write the polynomial as a product of linear factors.
X2 + 49
(Multiple Choice)
4.9/5  (32)
(32)
Use the given zero to find all the zeros of the function.
Function Zero
7x3 + 8x2 + 175x + 200 5i
(Multiple Choice)
4.8/5  (39)
(39)
Determine the equations of any horizontal and vertical asymptotes of .
(Multiple Choice)
4.9/5  (34)
(34)
Solve the equation and write complex solutions in standard form.
(Multiple Choice)
4.8/5  (28)
(28)
Determine the value that the function f approaches as the magnitude of x increases.
(Multiple Choice)
4.9/5  (33)
(33)
An open box is to be made from a square piece of material, 38 inches on a side, by cutting equal squares with sides of length x from the corners and turning up the sides (see figure) 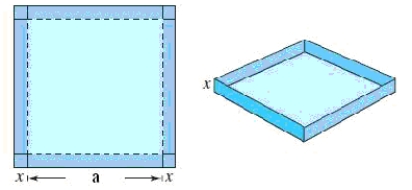 Where .
Determine the domain of the following function, V(x) represents the volume of the box .
Where .
Determine the domain of the following function, V(x) represents the volume of the box .
(Multiple Choice)
4.9/5  (35)
(35)
Find the values of b such that the function has the given maximum value 65.
(Multiple Choice)
4.9/5  (38)
(38)
Find all the rational zeros of the function.
X3 + 18x2 + 105x + 200
(Multiple Choice)
4.9/5  (33)
(33)
Solve the inequality and graph the solution on the real number line.
(Multiple Choice)
4.8/5  (38)
(38)
A rectangular playing field with a perimeter of 98 meters is to have an area of at least 444 square meters.Within what bounds must the length of the rectangle lie?
(Multiple Choice)
4.8/5  (34)
(34)
Determine the equations of any horizontal and vertical asymptotes of .
(Multiple Choice)
4.9/5  (36)
(36)
Find two positive real numbers whose product is a maximum.The sum is 140.
(Multiple Choice)
4.9/5  (41)
(41)
Showing 261 - 280 of 456
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)