Exam 2: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Solve the inequality and write the solution set in interval notation.
(Multiple Choice)
4.7/5  (45)
(45)
Find all real zeros of the polynomial and determine the multiplicity of each.
(Multiple Choice)
4.9/5  (37)
(37)
Find all the rational zeros of the function.
X3 - 7x2 + 14x - 8
(Multiple Choice)
4.9/5  (33)
(33)
Find all rational roots of the equation.
13x 3 - 2x 2 + 52x - 8 = 0
(Multiple Choice)
4.7/5  (32)
(32)
Simplify the complex number and write it in standard form.
(Multiple Choice)
4.7/5  (35)
(35)
Determine the value that the function f approaches as the magnitude of x increases.
(Multiple Choice)
4.7/5  (37)
(37)
Perform the operation and write the result in standard form.
(Multiple Choice)
4.8/5  (38)
(38)
An open box is to be made from a square piece of cardboard, 24 inches on a side, by cutting equal squares with sides of length x from the corners and turning up the sides (see figure below).If the volume of the box is represented by , determine the domain of . 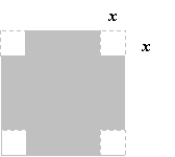
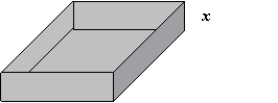
(Multiple Choice)
4.8/5  (45)
(45)
Showing 441 - 456 of 456
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)